
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{a•b}$ | C. | $\frac{2ab}{a+b}$ | D. | $\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$ |
分析 可利用三角换元求解.令m=$\sqrt{a}$cosα,n=$\sqrt{a}$sinα,x=$\sqrt{b}$cosβ,y=$\sqrt{b}$sinβ,将其代入mx+ny中,由三角函数公式和最值分析可得答案.
解答 解:令m=$\sqrt{a}$cosα,n=$\sqrt{a}$sinα,x=$\sqrt{b}$cosβ,y=$\sqrt{b}$sinβ,
则mx+ny=$\sqrt{ab}$cosαcosβ+$\sqrt{ab}$sinαsinβ=$\sqrt{ab}$cos(α-β)≤$\sqrt{ab}$,
当cos(α-β)=1时,取得最大值$\sqrt{ab}$.
故选B.
点评 本题主要考查求最值问题的解法,注意运用三角换元,注意利用基本不等式求最值的条件易忽略,属于中档题和易错题.


科目:高中数学 来源: 题型:选择题
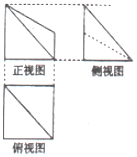 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” | |
| B. | 若p∨(¬q)为假命题,则p∧q为假命题 | |
| C. | “a≠5且b≠-5”是“a+b≠0”的充分不必要条件 | |
| D. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x0∈R,${x_0}^2+{x_0}+1=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5+ln2}{4}$ | B. | $\frac{5-ln2}{4}$ | C. | $\frac{3+ln2}{4}$ | D. | $\frac{3-ln2}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com