
���� ��1���������֪��c=1����Բ��������e=$\frac{c}{a}$=$\frac{1}{2}$���������a��b��ֵ�������Բ���̣�F2��1��0��Ϊ������C2��y2=4mx��m��0���Ľ���ɵ�m=1��
������������߷��̣�
��2����ֱ��б�ʴ棬��ֱ��AB�ķ���Ϊy=kx+n��������Բ���̣���Τ�ﶨ�����������������������㣬����������֪��7n2-12k2-12=0����OD��AB����$k=-\frac{x_0}{y_0}$����D��ֱ��AB�ϣ�y0=kx0+n��������õ�D�Ĺ켣����Ϊ${x^2}+{y^2}=\frac{12}{9}��y��0��$����ֱ��AB��б�ʲ�����ʱ��$D����\frac{{2\sqrt{21}}}{7}��0��������{x^2}+{y^2}=\frac{12}{7}$��������õ�DΪ�켣���̣�
��� �⣺��1��������֪��ԲC1��F2��1��0����c=1��
����Բ��������e=$\frac{c}{a}$=$\frac{1}{2}$
��$a=2��b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$
����Բ�ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{3}$=1����2�֣�
��F2��1��0��Ϊ������C2��y2=4mx��m��0���Ľ���ɵ�m=1��
�������ߵķ���Ϊy2=4x����4�֣�
��2����ֱ��AB��б��k����ʱ
��ֱ��AB�ķ���Ϊy=kx+n����A��x1��y1����B��x2��y2��
����$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+n\end{array}\right.$��
�ã�4k2+3��x2+8knx+4n2-12=0����6�֣�
��${x_1}+{x_2}=-\frac{8kn}{{4{k^2}+3}}��{x_1}{x_2}=\frac{{4{n^2}-12}}{{4{k^2}+3}}$��
��${y_1}{y_2}=��k{x_1}+n����k{x_2}+n��={k^2}{x_1}{x_2}+kn��{x_1}+{x_2}��+{n^2}$��
��$\overrightarrow{OA}•\overrightarrow{OB}=0$��
��x1x2+y1y2=0��
��$��{k^2}+1��{x_1}{x_2}+kn��{x_1}+{x_2}��+n=0��\frac{{\{{k^2}+1\}��4{n^2}-12��}}{{4{k^2}+3}}-\frac{{8{k^2}{n^2}}}{{4{k^2}+3}}+{n^2}=0$��
��7n2-12k2-12=0�١���8�֣�
�֡�OD��AB����D��x0��y0����
��$k=-\frac{x_0}{y_0}$��
�֡ߵ�D��ֱ��AB�ϣ�
��y0=kx0+n��
��$n={y_0}-k{x_0}={y_0}+\frac{x_0^2}{y_0}$�ۡ���10�֣�
�Ѣڢ۴���ٵ�$7{��{y_0}+\frac{x_0^2}{y_0}��^2}-12\frac{x_0^2}{y_0^2}-12=0$��
��$\frac{x_0^2+y_0^2}{y_0^2}[7��x_0^2+y_0^2��-12]=0$��
��$x_0^2+y_0^2=\frac{12}{7}$��
���D�Ĺ켣����Ϊ${x^2}+{y^2}=\frac{12}{9}��y��0��$��
��ֱ��AB��б�ʲ�����ʱ��$D����\frac{{2\sqrt{21}}}{7}��0��������{x^2}+{y^2}=\frac{12}{7}$
���D�Ĺ켣����Ϊ${x^2}+{y^2}=\frac{12}{7}$����13�֣�
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������켣���̵���Τ�ﶨ���������������������ʾ��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
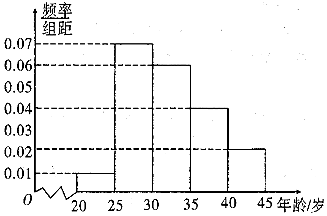 ��һ��һ·���ǡ�˿��֮·���ô����͡�21���ͺ���˿��֮·���ļ�ƣ�ij��Ϊ���˽����Ƕԡ�һ��һ·������֪�̶ȣ��Բ�ͬ����Ͳ�ְͬҵ���˾ٰ���һ�Ρ�һ��һ·��֪ʶ����������100�֣�90�ּ�����Ϊ��֪�̶ȸߣ����ִӲ������г�ȡ��x�ˣ�������ֳ�5�飨��һ�飺[20��25�����ڶ��飺[25��30���������飺[30��35���������飺[35��40���������飺[40��45]�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪��һ����6�ˣ�
��һ��һ·���ǡ�˿��֮·���ô����͡�21���ͺ���˿��֮·���ļ�ƣ�ij��Ϊ���˽����Ƕԡ�һ��һ·������֪�̶ȣ��Բ�ͬ����Ͳ�ְͬҵ���˾ٰ���һ�Ρ�һ��һ·��֪ʶ����������100�֣�90�ּ�����Ϊ��֪�̶ȸߣ����ִӲ������г�ȡ��x�ˣ�������ֳ�5�飨��һ�飺[20��25�����ڶ��飺[25��30���������飺[30��35���������飺[35��40���������飺[40��45]�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪��һ����6�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a+b}{2}$ | B�� | $\sqrt{a•b}$ | C�� | $\frac{2ab}{a+b}$ | D�� | $\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 4�� | C�� | 8�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | 1��-$\frac{1}{2}$ | D�� | -1��$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com