
| 鱼的重量 | [1.00,1.05) | [1.05,1.10) | [1.10,1.15) | [1.15,1.20) | [1.20,1.25) | [1.25,1.30) |
| 鱼的条数 | 3 | 20 | 35 | 31 | 9 | 2 |
分析 (1)捕捞的100条鱼中间,求出数据落在[1.20,1.25)的概率,再求出数据落在[1.20,1.30)中的概率,相加即得所求.
(2)重量在[1.00,1.05)的鱼有3条,把这3条鱼分别记作A1,A2,A3,重量在[1.25,1.30)的鱼有2条,分别记作:B1,B2,写出所有的可能选法,再找出满足条件的选法,从而求得所求事件的概率.
解答 解:(1)捕捞的100条鱼中,数据落在[1.20,1.30)中的概率约为P1=$\frac{9+2}{100}$=0.11,
由于0.11×100%=11%<15%,故饲养的这批鱼没有问题.
(2)重量在[1.00,1.05)的鱼有3条,把这3条鱼分别记作A1,A2,A3,
重量在[1.25,1.30)的鱼有2条,分别记作B1,B2,
那么从中任取2条的所有的可能有:
{A1,A2},{A1,A3},{A1,B1},{A1,B2},
{A2,A3},{A2,B1},{A2,B2},{A3,B1},
{A3,B2},{B1,B2}共10种.
而恰好所取得鱼的重量在[1.00,1.05)和[1.25,1.30)中各有1条的情况有:
{A1,B1},{A1,B2},{A2,B1},
{A2,B2},{A3,B1},{A3,B2},共6种.
所以恰好所取得鱼的重量在[1.00,1.05)和[1.25,1.30)中各有1条的概率p=$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题主要考查用列举法求基本事件及事件发生的概率,属于基础题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
| 有过粉尘环境工作经历 | 无粉尘环境工作经历 | 合计 | |
| 有尘肺病 | 22 | 2 | 24 |
| 无尘肺病 | 898 | 1498 | 2396 |
| 合计 | 920 | 1500 | 2420 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a | B. | a-2 | C. | $\root{3}{a^4}$ | D. | a4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
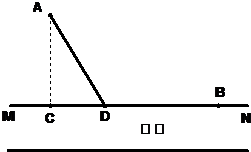 有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?
有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com