
分析 数列{an}当n≥2时满足$\frac{2}{{a}_{n}}$=$\frac{1}{{a}_{n-1}}$+$\frac{1}{{a}_{n+1}}$,可得数列$\{\frac{1}{{a}_{n}}\}$是等差数列,设公差为d.由$\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{7}}$=9,可得$\frac{3}{{a}_{5}}$=9,解得$\frac{1}{{a}_{5}}$=3.由a3a5a7=$\frac{1}{24}$,可得$\frac{1}{{a}_{3}{a}_{5}{a}_{7}}$=24,因此(3-2d)×3×(3+2d)=24,解出d,进而得出.
解答 解:∵数列{an}当n≥2时满足$\frac{2}{{a}_{n}}$=$\frac{1}{{a}_{n-1}}$+$\frac{1}{{a}_{n+1}}$,
∴数列$\{\frac{1}{{a}_{n}}\}$是等差数列,设公差为d.
∵$\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{7}}$=9,
∴$\frac{3}{{a}_{5}}$=9,解得$\frac{1}{{a}_{5}}$=3.
∵a3a5a7=$\frac{1}{24}$,∴$\frac{1}{{a}_{3}{a}_{5}{a}_{7}}$=24,
∴(3-2d)×3×(3+2d)=24,
解得d=$±\frac{1}{2}$.
d=$\frac{1}{2}$时,$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{5}}$+(n-5)d=3+$\frac{1}{2}(n-5)$=$\frac{n+1}{2}$.
∴S4=$\frac{2+3+4+5}{2}$=7.
d=-$\frac{1}{2}$时,$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{5}}$+(n-5)d=3-$\frac{1}{2}(n-5)$=$\frac{11-n}{2}$.(舍去,n=11时不存在).
综上可得:S4=7.
故答案为:7.
点评 本题考查了等差数列的通项公式及其求和公式与性质,考查了推理能力与计算能力,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (?p)∧(?q) | D. | (?p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | a<b<c | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
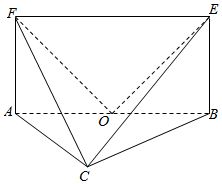 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com