
 从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人
从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人分析 (Ⅰ)抽取的m名学生中星期日运动时间少于60分钟的概率为:($\frac{1}{750}$+$\frac{1}{3000}$)×30=$\frac{1}{20}$,由此能够求出m的值并求出星期日运动时间在[90,120]内的概率.
(Ⅱ)由题设ξ的所有可能取值为0,1,2,3,分别求出其概率,能够得到ξ的分布列和Eξ.
解答 解:(Ⅰ)抽取的m名学生中星期日运动时间少于60分钟的概率为:($\frac{1}{750}$+$\frac{1}{3000}$)×30=$\frac{1}{20}$,
∴m×$\frac{1}{20}$=5,
∴m=100
∴星期日运动时间在[90,120]内的概率为1-($\frac{1}{3000}$+$\frac{1}{750}$+$\frac{1}{300}$+$\frac{1}{100}$+$\frac{1}{200}$+$\frac{1}{300}$+$\frac{1}{600}$)×30=$\frac{1}{4}$;
(Ⅱ)由图知:第一组1人,第二组4人,第七组10人,第八组5人,总计20人.
则ξ的所有可能取值为0,1,2,3,P(ξ=i)=$\frac{{C}_{5}^{i}{C}_{15}^{3-i}}{{C}_{20}^{3}}$,(i=0,1,2,3),
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{91}{228}$ | $\frac{35}{76}$ | $\frac{5}{38}$ | $\frac{1}{114}$ |
点评 本题考查了频率分布直方图的应用问题,考查了离散型随机事件的分布列与数学期望的计算问题,考查了计算能力的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
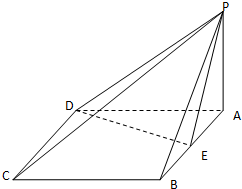 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com