Question

2．设椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上存在一点P，它与两焦点连线互相垂直，求m的取值范围．

Answer 1

分析 根据椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上至少存在一点P，使得它与两焦点连线互相垂直，结合椭圆的性质得：∠F₁AF₂≥90°，即OA≤$\frac{\sqrt{2}}{2}$AF₂，从而得出正实数m的取值范围．

解答 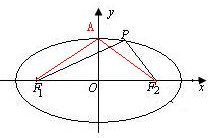解：如图，∵椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上至少存在一点P，使得它与两焦点连线互相垂直，
设椭圆的上顶点为A，
结合椭圆的性质得：∠F₁AF₂≥90°，
∴∠OAF₂≥45°，
即OA≤$\frac{\sqrt{2}}{2}$AF₂，⇒0＜m≤$\frac{1}{2}$（m+25）⇒0＜m≤25，
则正实数m的取值范围为（0，25]．
故答案为：（0，25]．

点评 本题主要考查了直线与圆锥曲线的综合问题．考查了学生综合分析问题和数形结合能力．