
分析 (1)如图所示,设点P(x0,y0),A(x1,y1),B(x2,y2),可得直线AB的方程为${x}_{0}x+{y}_{0}y={b}^{2}$.由2b=8,可得直线AB的方程为x0x+y0y=16.可得M$(\frac{16}{{x}_{0}},0)$,N$(0,\frac{16}{{y}_{0}})$,|OM|=$\frac{16}{|{x}_{0}|}$,|ON|=$\frac{16}{|{y}_{0}|}$,代入$\frac{{a}^{2}}{|OM{|}^{2}}$+$\frac{{b}^{2}}{|ON{|}^{2}}$=$\frac{25}{16}$,可得$\frac{{a}^{2}{x}_{0}^{2}}{1{6}^{2}}+\frac{{y}_{0}^{2}}{16}=\frac{25}{16}$,又$\frac{{y}_{0}^{2}}{{a}^{2}}+\frac{{x}_{0}^{2}}{16}=1$,联立可得a2=25,即可得出椭圆方程.
(2)假设存在点P(x0,y0)满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,连接OA,OB,由|PA|=|PB|,可知:四边形PAOB为正方形,|OP|=$\sqrt{2}$|OA|,${x}_{0}^{2}+{y}_{0}^{2}=2{b}^{2}$,又点P在椭圆上,可得${a}^{2}{x}_{0}^{2}+{b}^{2}{y}_{0}^{2}={a}^{2}{b}^{2}$,联立${x}_{0}^{2}$,${y}_{0}^{2}$,即可得出体积.
解答 解:(1)如图所示, 设点P(x0,y0),A(x1,y1),B(x2,y2),
设点P(x0,y0),A(x1,y1),B(x2,y2),
则切线PA的方程为:${x}_{1}x+{y}_{1}y={b}^{2}$,切线PB的方程为:${x}_{2}x+{y}_{2}y={b}^{2}$,
∴直线AB的方程为${x}_{0}x+{y}_{0}y={b}^{2}$.
∵2b=8,∴b=4,
∴直线AB的方程为x0x+y0y=16.
可得M$(\frac{16}{{x}_{0}},0)$,N$(0,\frac{16}{{y}_{0}})$,
∴|OM|=$\frac{16}{|{x}_{0}|}$,|ON|=$\frac{16}{|{y}_{0}|}$,代入$\frac{{a}^{2}}{|OM{|}^{2}}$+$\frac{{b}^{2}}{|ON{|}^{2}}$=$\frac{25}{16}$,可得$\frac{{a}^{2}{x}_{0}^{2}}{1{6}^{2}}+\frac{{y}_{0}^{2}}{16}=\frac{25}{16}$,(*)
又点P在椭圆上,∴$\frac{{y}_{0}^{2}}{{a}^{2}}+\frac{{x}_{0}^{2}}{16}=1$,
变形为${y}_{0}^{2}=(1-\frac{{x}_{0}^{2}}{16}){a}^{2}$,代入(*)可得a2=25,
故所求椭圆方程为:$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{16}=1$(xy≠0).
(2)假设存在点P(x0,y0)满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,连接OA,OB,
由|PA|=|PB|,可知:四边形PAOB为正方形,|OP|=$\sqrt{2}$|OA|,
∴${x}_{0}^{2}+{y}_{0}^{2}=2{b}^{2}$,
又点P在椭圆上,∴${a}^{2}{x}_{0}^{2}+{b}^{2}{y}_{0}^{2}={a}^{2}{b}^{2}$,
联立$\left\{\begin{array}{l}{{x}_{0}^{2}+{y}_{0}^{2}=2{b}^{2}}\\{{a}^{2}{x}_{0}^{2}+{b}^{2}{y}_{0}^{2}={a}^{2}{b}^{2}}\end{array}\right.$,解得${x}_{0}^{2}$=$\frac{{b}^{2}({a}^{2}-2{b}^{2})}{{a}^{2}-{b}^{2}}$,${y}_{0}^{2}$=$\frac{{a}^{2}{b}^{2}}{{a}^{2}-{b}^{2}}$,
∵a>b>0,a2>b2>0,
∴当a2≥2b2>0时,即$a≥\sqrt{2}b$时,椭圆C上存在满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0的点P.
当a2<2b2时,椭圆C上不存在满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0的点P.
点评 本题考查了椭圆与圆的标准方程及其性质、直线与圆相切的切线问题、正方形的性质、垂直与数量积的关系,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
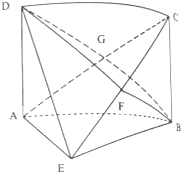 如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.
如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
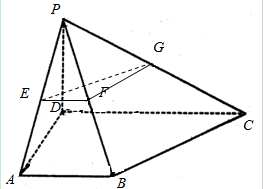 如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.
如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com