考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用
分析:(1)先求f(x)的定义域,知道定义域关于原点对称,然后容易求得f(-x)=-f(x),所以得到函数f(x)为奇函数;
(2)可以用两种方法讨论f(x)的单调性:第一种方法,可以用导数法,求f′(x),通过解f′(x)≥0,f′(x)<0即可得到f(x)的单调区间,即判断出f(x)的单调性;第二种方法,用单调性的定义,在定义域上任取x1,x2,且x1<x2,通过作差比较f(x1),f(x2)的大小,从而得出f(x)的单调区间,从而判断出f(x)的单调性.
解答:
解:(1)f(x)的定义域为{x|x≠0};
f(-x)=-x-
=-f(x);
∴f(x)为奇函数;
(2)方法(一):
f′(x)=1
-=;
∴x
∈[-,0)或(0,]时,f′(x)≤0,∴f(x)在
[-,0),(0,]上单调递减;
x
∈(-∞,-),或(,+∞)时,f′(x)>0,∴f(x)在(
-∞,-),
(,+∞)上单调递增;
方法(二):
设x
1,x
2∈{x|x≠0},且x
1<x
2,则:
f(x
1)-f(x
2)=
x1-x2+-=(x1-x2)(1-)=
(x1x2-a);
∴①
x1,x2∈[-,0),或(0,]时,x
1x
2-a≤0,x
1x
2>0,x
1-x
2<0;
∴f(x
1)>f(x
2);
∴f(x)在
[-,0),(0,]上单调递减;
②
x1,x2∈(-∞,-),或(,+∞)时,x
1x
2-a>0,x
1x
2>0,x
1-x
2<0;
∴f(x
1)<f(x
2);
∴f(x)在(-∞,-
),(
,+∞)上单调递增.
点评:考查奇函数的定义,以及判断一个函数奇偶性的过程,根据导数符号判断函数单调性的方法,以及单调性的定义及利用定义判断函数的单调性的过程.



 巧学巧练系列答案
巧学巧练系列答案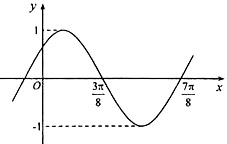 已知函数y=sin(ωx+φ)(ω>0,|φ|<
已知函数y=sin(ωx+φ)(ω>0,|φ|<