
分析 (1)首先设P(x,y),由题意知M与P的关系,再由M是曲线C1上的动点,求出点P的参数方程,即:$\left\{\begin{array}{l}{x=4+4cosα}\\{y=4sinα}\end{array}\right.$ (α为参数),从而得到C2的轨迹方程为:(x-4)2+y2=16.
(2)为了求出线段AB的长度,首先把把曲线C1的方程转化为极坐标方程为:ρ=4cosθ,再把曲线C2方程转化为的极坐标方程为:ρ=8cosθ,最后利用射线$θ=\frac{π}{6}$与C1的交点A的极径为${ρ}_{1}=4cos\frac{π}{6}$,射线$θ=\frac{π}{6}$与C2的交点B的极径为.${ρ}_{2}=8cos\frac{π}{6}$,最终求出线段AB的长度.
解答 解:(1)设P(x,y),由题意知M($\frac{x}{2}$,$\frac{y}{2}$),M是曲线C1上的动点,
所以:$\left\{\begin{array}{l}{\frac{x}{2}=2+2cosα}\\{\frac{y}{2}=2sinα}\end{array}\right.$(α为参数),
整理得:$\left\{\begin{array}{l}{x=4+4cosα}\\{y=4sinα}\end{array}\right.$ (α为参数),
从而C2的轨迹方程为:(x-4)2+y2=16.
(2)依题意把曲线C1的方程转化为极坐标方程为:ρ=4cosθ,
曲线C2方程转化为的极坐标方程为:ρ=8cosθ,
射线$θ=\frac{π}{6}$与C1的交点A的极径为${ρ}_{1}=4cos\frac{π}{6}$,
射线$θ=\frac{π}{6}$与C2的交点B的极径为.${ρ}_{2}=8cos\frac{π}{6}$,
所以:|AB|=|ρ1-ρ2|=2$\sqrt{3}$.
点评 本题考查的知识点,参数方程及极坐标方程与普通方程的互化,利用极径求线段的长度,属于基础题型.


科目:高中数学 来源: 题型:选择题
 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )| A. |  | B. |  | C. |  | D. | 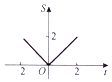 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2π}{3}$) | B. | (0,π) | C. | ($\frac{π}{3}$,$\frac{2π}{3}$) | D. | ($\frac{2π}{3}$π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{14}{3}\sqrt{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{{7\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 12立方丈 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com