
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() (a﹣ccosB)=bsinC.
(a﹣ccosB)=bsinC.
(1)求角C的大小;
(2)若c=2,则当a,b分别取何值时,△ABC的面积取得最大值,并求出其最大值.
【答案】
(1)解:∵ ![]() (a﹣ccosB)=bsinC,由正弦定理可得:
(a﹣ccosB)=bsinC,由正弦定理可得: ![]() (sinA﹣sinCcosB)=sinBsinC,
(sinA﹣sinCcosB)=sinBsinC,
化为: ![]() [sin(B+C)﹣sinCcosB]=
[sin(B+C)﹣sinCcosB]= ![]() sinBcosC=sinBsinC,
sinBcosC=sinBsinC,
∵sinB≠0,
∴tanC= ![]() ,
,
∵C∈(0,π),
∴C= ![]() .
.
(2)解:c=2,C= ![]() ,由余弦定理可得:c2=a2+b2﹣2abcos
,由余弦定理可得:c2=a2+b2﹣2abcos ![]() ,
,
∴4≥2ab﹣ab=ab>0,当且仅当a=b=2时取等号.
又S△ABC= ![]() sin
sin ![]() =
= ![]() ab≤
ab≤ ![]() ,当且仅当a=b=2时取等号
,当且仅当a=b=2时取等号
【解析】(1) ![]() (a﹣ccosB)=bsinC,由正弦定理可得:
(a﹣ccosB)=bsinC,由正弦定理可得: ![]() (sinA﹣sinCcosB)=sinBsinC,由sinB≠0,展开可得tanC=
(sinA﹣sinCcosB)=sinBsinC,由sinB≠0,展开可得tanC= ![]() ,即可得出.(2)由余弦定理可得:c2=a2+b2﹣2abcos
,即可得出.(2)由余弦定理可得:c2=a2+b2﹣2abcos ![]() ,再利用基本不等式的性质可得:4≥ab>0,S△ABC=
,再利用基本不等式的性质可得:4≥ab>0,S△ABC= ![]() sin
sin ![]() =
= ![]() ab即可得出.
ab即可得出.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三个内角A,B,C的对边,向量 ![]() =(﹣1,
=(﹣1, ![]() ),
), ![]() =(cosA,sinA).若
=(cosA,sinA).若 ![]() ⊥
⊥ ![]() ,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,且acosB+bcosA=csinC,则角A,B的大小分别为( )
A.![]() ,
, ![]()
![]()
B.![]() ,
, ![]()
![]()
C.![]() ,
, ![]()
![]()
D.![]() ,
, ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从向阳小区抽取100户居民进行月用电量调查,为制定阶梯电价提供数据,发现其用电量都在50到350度之间,制作频率分布直方图的工作人员粗心大意,位置t处未标明数据,你认为t=( ) 
A.0.0041
B.0.0042
C.0.0043
D.0.0044
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角三角形ABC中角A,B,C对边长分别为a,b,c,∠C=90°.
(1)若三角形面积为2,求斜边长c最小值;
(2)试比较an+bn与cn(n∈N*)的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
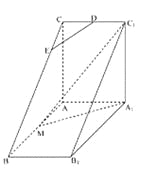
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 为增函数,对任意
为增函数,对任意![]() 都有
都有![]() (
(![]() 为常数)
为常数)
(1)判断![]() 为何值时,
为何值时,![]() 为奇函数,并证明;
为奇函数,并证明;
(2)设![]() ,
,![]() 是
是![]() 上的增函数,且
上的增函数,且![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)若![]() ,
,![]() ,
,![]() 为
为![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于y=3sin(2x﹣ ![]() )有以下命题:
)有以下命题:
①f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z);
②函数的解析式可化为y=3cos(2x﹣ ![]() );
);
③图象关于x=﹣ ![]() 对称;④图象关于点(﹣
对称;④图象关于点(﹣ ![]() ,0)对称.
,0)对称.
其中正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com