
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 画出函数f(x)=x2+ax+blnx+c的草图,结合f[f(x)]=0时,f(x)=x1,或f(x)=x2,或f(x)=x3,可得答案.
解答 解:∵函数f(x)=x2+ax+blnx+c有三个不同的零点x1,x2,x3且x1<x2<x3的若x=m是f(x)的极大值点,且f(m)=x3,
则函数f(x)的图象如下图所示: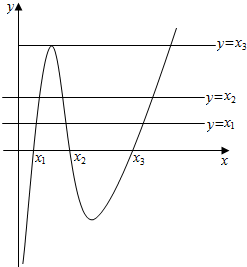
若f[f(x)]=0,则f(x)=x1,或f(x)=x2,或f(x)=x3,
由图可得:f(x)=x1有3个根;
f(x)=x2有3个根;
f(x)=x3有2个根;
故方程f[f(x)]=0有8个根,
故选:D.
点评 本题考查的知识点是方程的根与函数的零点,数形结合思想,难度中档.


科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
函数y=sin(2x+ )的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )
)的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )
A.向右平移 B.向左平移
B.向左平移
C.向右平移 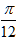 D.向左平移
D.向左平移 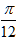
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | -5 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com