已知数列{an}为等差数列.a2=2且满足a2.a3.a5成等比数列.则数列{an}的前10项的和为( )A．80B．90C．20D．20或90 题目和参考答案——青夏教育精英家教网—

14．已知数列{a_n}为等差数列，a₂=2且满足a₂，a₃，a₅成等比数列，则数列{a_n}的前10项的和为（　　）

A．

B．

C．

D．

20或90

分析先根据等比中项的性质求出公差d，再根据等差数列的前n项和公式计算即可．

解答解：a₂，a₃，a₅成等比数，
∴（a₂+d）²=a₂•（a₂+3d），
∴（2+d）²=2•（2+3d），
解得d=0或d=2，
∴a₁=2，或a₁=0，
当d=0时，S₁₀=10a₁=20，
当d=2，S₁₀=10a₁+$\frac{10（10-1）×2}{2}$=90，
故选：D．

点评本题考查了等差数列的通项公式和前n项和公式，属于基础题．

练习册系列答案

欢乐寒假福建教育出版社系列答案

智多星寒假生活新疆美术摄影出版社系列答案

快乐假期高考状元假期学习方案寒假系列答案

创新学习寒假作业东北师范大学出版社系列答案

寒假零距离系列答案

高效中考安徽师范大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

4．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x，则此双曲线的离心率为（　　）

A．

$\sqrt{3}$

B．

$\sqrt{2}$

C．

$\frac{\sqrt{6}}{2}$

D．

$\frac{3}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

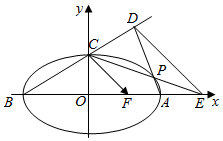如图：A，B，C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的顶点，点F（c，0）为椭圆的右焦点，原点O到直线CF的距离为$\frac{1}{2}c$，且椭圆过点$（{2\sqrt{3}，1}）$．
（Ⅰ）求椭圆的方程；
（Ⅱ）若P是椭圆上除顶点外的任意一点，直线CP交x轴于点E，直线BC与AP相交于点D，连结DE．设直线AP的斜率为k，直线DE的斜率为k₁，问是否存在实数λ，使得$λ{k_1}=k+\frac{1}{2}$成立，若存在求出λ的值，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．

某人在连续7天的定点投篮的分数统计如下：在上述统计数据的分析中，一部分计算如右图所示的算法流程图（其中$\overline{a}$是这7个数据的平均数），则输出的S的值是（　　）

观测次数i	1	2	3	4	5	6	7
观测数据a_i	5	6	8	6	8	8	8

A．

B．

$\frac{8}{7}$

C．

$\frac{9}{7}$

D．

$\frac{10}{7}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F₂，M是双曲线C在第一象限上一点，N与M关于原点对称，MF₂交双曲线C于另一点P，NF₂⊥PF₂，|NF₂|=|PF₂|，则双曲线C的渐近线为y=±$\frac{\sqrt{6}}{2}$x．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．设复数z满足（z-1）（1+i）=2（i为虚数单位），则|z|=（　　）

A．

B．

C．

$\sqrt{5}$

D．

$\sqrt{13}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．如图所示的算法框图中，e是自然对数的底数，则输出的i的值为（参考数值：ln2016≈7.609）（　　）