
分析 本题要先安排乙和丙两人,其安排方法可以分为两类,一类是两者之一在A社区,另一个在B社区,另一类是两者都在B社区,在每一类中用分步原理计算种数即可.
解答 解:若乙和丙两人有一人在A社区,另一人在B社区,则第一步安排A社区有2种安排方法,第二步安排B社区,从三人中选一人有三种方法,第二步余下两人去C社区,一种方法;
故此类中安排方法种数是2×3=6,
若乙和丙两人在B社区,第一步安排A社区,有三种安排方法,第二步安排C社区,余下两人去B社区,一种安排方法,故总的安排方法有3×1=3,
综上,总的安排方法种数有6+3=9种;
故答案为:9.
点评 本题考查分步原理与分类原理的应用,求解本题关键是根据实际情况选择正确的分类标准与分步标准,把实际问题的结构理解清楚.


科目:高中数学 来源: 题型:选择题
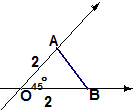
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{32}$+$\frac{y^2}{16}$=1 | B. | $\frac{x^2}{12}$+$\frac{y^2}{8}$=1 | C. | $\frac{x^2}{8}$+$\frac{y^2}{4}$=1 | D. | $\frac{x^2}{12}$+$\frac{y^2}{4}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com