Question

12．函数f（x）=|x²-a²+$\frac{1}{2}$a|在区间[-$\sqrt{3}$，$\sqrt{3}$]上的最大值M（a）取最小值时a=-$\frac{3}{2}$或2．

Answer 1

分析 通过分类讨论去掉绝对值符号，进而通过函数f（x）图象与x轴有两个交点时，利用对称性比较交点与区间端点的位置关系，进而计算可得函数M（a）的表达式，然后数形结合即得结论．

解答 解：依题意，函数f（x）的图象关于y轴对称，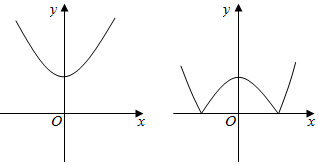

（1）若-a²+$\frac{1}{2}$a≥0即0≤a≤$\frac{1}{2}$时，此时M（a）=f（$\sqrt{3}$）=3-a²+$\frac{1}{2}$a；
（2）若-a²+$\frac{1}{2}$a＜0即a＜0或a＞$\frac{1}{2}$时，
此时函数f（x）与x轴有两个交点，其横坐标为±$\sqrt{{a}^{2}-\frac{1}{2}a}$，
①当交点在区间[-$\sqrt{3}$，$\sqrt{3}$]外时，则$\sqrt{3}$＜$\sqrt{{a}^{2}-\frac{1}{2}a}$，
解得：a＜-$\frac{3}{2}$或a＞2，
此时M（a）=f（0）=a²-$\frac{1}{2}$a；
②当交点在区间[-$\sqrt{3}$，$\sqrt{3}$]内时，$\sqrt{3}$≥$\sqrt{{a}^{2}-\frac{1}{2}a}$，
解得：-$\frac{3}{2}$≤a≤2，
故当-$\frac{3}{2}$≤a＜0或$\frac{1}{2}$＜a≤2时M（a）为f（0）与f（$\sqrt{3}$）中最大者，
又∵f（$\sqrt{3}$）=3-a²+$\frac{1}{2}$a，f（0）=a²-$\frac{1}{2}$a，
∴方程f（$\sqrt{3}$）=f（0）的解为：a=-1或a=$\frac{3}{2}$，
则当-$\frac{3}{2}$≤a＜-1或$\frac{3}{2}$＜a≤2时，M（a）=f（$\sqrt{3}$）=3-a²+$\frac{1}{2}$a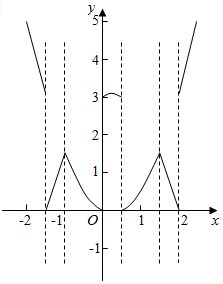

当-1≤a＜0或$\frac{1}{2}$＜a≤$\frac{3}{2}$时，M（a）=f（0）=a²-$\frac{1}{2}$a；
综上所述，M（a）=$\left\{\begin{array}{l}{{a}^{2}-\frac{1}{2}a，}&{a＜-\frac{3}{2}}\\{3-{a}^{2}+\frac{1}{2}a，}&{-\frac{3}{2}≤a＜-1}\\{{a}^{2}-\frac{1}{2}a，}&{-1≤a＜0}\\{3-{a}^{2}+\frac{1}{2}a，}&{0≤a≤\frac{1}{2}}\\{{a}^{2}-\frac{1}{2}a，}&{\frac{1}{2}＜a≤\frac{3}{2}}\\{3-{a}^{2}+\frac{1}{2}a，}&{\frac{3}{2}＜a≤2}\\{{a}^{2}-\frac{1}{2}a，}&{a＞2}\end{array}\right.$，
结合图象易知M（a）取最小值时a=-$\frac{3}{2}$或a=2，
故答案为：-$\frac{3}{2}$或2．

点评 本题考查函数的最值及其几何意义，考查数形结合能力，考查分类讨论的思想，注意解题方法的积累，属于中档题．