
分析 (1)利用商品的月销售额等于月销售量与价格的乘积,分类讨论,即可求解商品的价格为多少时,该商品的月销售额最大?
(2)设f(x)=y1-y2=ax+$\frac{7}{2}$a2-a-(-$\frac{1}{224}$x2-$\frac{1}{112}$x+1)=$\frac{1}{224}$x2+($\frac{1}{112}$+a)x+$\frac{7}{2}$a2-a-1,因为a>0,所以f(x)在区间(1,14)上是增函数,若该商品的均衡价格不低于6百元,即函数f(x)在区间[6,14)上有零点,即可得出结论.
解答 解:(1)若a=$\frac{1}{7}$,y1=$\frac{1}{7}$x-$\frac{1}{14}$,
y2>y1,即-$\frac{1}{224}$x2-$\frac{1}{112}$x+1>$\frac{1}{7}$x-$\frac{1}{14}$,∵1<x<14,∴1<x<6,月销售量为y1=$\frac{1}{7}$x-$\frac{1}{14}$,
商品的月销售额等于($\frac{1}{7}$x-$\frac{1}{14}$)x,在(1,6)上单调递增,($\frac{1}{7}$x-$\frac{1}{14}$)x<$\frac{33}{7}$;
y2≤y1,即-$\frac{1}{224}$x2-$\frac{1}{112}$x+1≤$\frac{1}{7}$x-$\frac{1}{14}$,∵1<x<14,∴6≤x<14,月销售量为y2=-$\frac{1}{224}$x2-$\frac{1}{112}$x+1,
商品的月销售额等于y=(-$\frac{1}{224}$x2-$\frac{1}{112}$x+1)x,y′=-$\frac{1}{224}$(x-8)(3x+28),
∴函数在(6,8)上单调递增,(8,14)上单调递减,x=8时,取得最大值$\frac{36}{7}$>$\frac{33}{7}$,
∴商品的价格为8百元时,该商品的月销售额最大;
(2)设f(x)=y1-y2=ax+$\frac{7}{2}$a2-a-(-$\frac{1}{224}$x2-$\frac{1}{112}$x+1)=$\frac{1}{224}$x2+($\frac{1}{112}$+a)x+$\frac{7}{2}$a2-a-1
因为a>0,所以f(x)在区间(1,14)上是增函数,
若该商品的均衡价格不低于6百元,即函数f(x)在区间[6,14)上有零点,
所以f(6)≤0,f(14)>0,?
所以0<a≤$\frac{1}{7}$.
点评 本题考查函数知识的运用,考查函数的单调性,考查学生利用数学知识解决实际问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 在平面α内没有直线与直线a垂直 | |
| B. | 在平面α内有且只有一条直线与直线a垂直 | |
| C. | 在平面α内有无数条直线与直线a垂直 | |
| D. | 在平面α内存在两条相交直线与直线a垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )| A. | y=2sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=2sin($\frac{π}{3}$x+$\frac{5π}{6}$) | C. | y=2sin($\frac{π}{2}$x+$\frac{π}{6}$) | D. | y=2sin($\frac{π}{2}$x+$\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
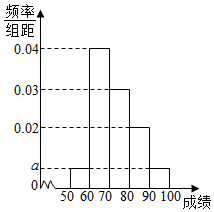 某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生其中考试数学成绩的频率分布直方图如图所示,其中成绩分布区间是[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com