
分析 (Ⅰ)由椭圆右焦点F($\sqrt{2}$,0),点D($\sqrt{2}$,1)在椭圆上,列出方程组,求出a,b,由此能求出椭圆C的标准方程.
(Ⅱ)设A(x1,y1),则B(-x1,-y1),设P(2cosθ,$\sqrt{2}$sinθ),则 kPA•kPA=$\frac{{{y}_{1}}^{2}-2si{n}^{2}θ}{{{x}_{1}}^{2}-4co{s}^{2}θ}$,由此能推导出kPA•kPB为定值.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点F($\sqrt{2}$,0),点D($\sqrt{2}$,1)在椭圆上,
∴$\left\{\begin{array}{l}{c=\sqrt{2}}\\{\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=2,
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1.
(Ⅱ)设A(x1,y1),∵直线l:y=kx与椭圆C交于A,B两点,∴点A、B关于原点O对称,∴B(-x1,-y1).
∵P为椭圆C上异于A,B的动点,∴设P(2cosθ,$\sqrt{2}$sinθ),
则 kPA=$\frac{{y}_{1}-\sqrt{2}sinθ}{{x}_{1}-2cosθ}$,kPA=$\frac{-{y}_{1}-\sqrt{2}sinθ}{-{x}_{1}-2cosθ}$=$\frac{{{y}_{1}+\sqrt{2}sinθ}^{\;}}{{x}_{1}+2cosθ}$,
∴kPPA•kPA=$\frac{{y}_{1}-\sqrt{2}sinθ}{{x}_{1}-2cosθ}$•$\frac{{{y}_{1}+\sqrt{2}sinθ}^{\;}}{{x}_{1}+2cosθ}$=$\frac{{{y}_{1}}^{2}-2si{n}^{2}θ}{{{x}_{1}}^{2}-4co{s}^{2}θ}$,
∵A在椭圆上,∴$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}$=1,∴${{y}_{1}}^{2}$=2(1-$\frac{{{x}_{1}}^{2}}{4}$),
∴kPA•kPA=$\frac{2(1-\frac{{{x}_{1}}^{2}}{4})-2si{n}^{2}θ}{{{x}_{1}}^{2}-4co{s}^{2}θ}$=$\frac{2co{s}^{2}θ-\frac{{{x}_{1}}^{2}}{2}}{{{x}_{1}}^{2}-4co{s}^{2}θ}$=-$\frac{1}{2}$,
∴kPA•kPB为定值-$\frac{1}{2}$.
点评 本题考查椭圆的标准方程的求法,考查两直线的斜率之积是否为定值的判断与求法,是中档题,解题时要认真审题,注意椭圆的对称性质和参数方程的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )| A. | y=2sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=2sin($\frac{π}{3}$x+$\frac{5π}{6}$) | C. | y=2sin($\frac{π}{2}$x+$\frac{π}{6}$) | D. | y=2sin($\frac{π}{2}$x+$\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
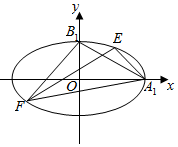 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com