
如图,将边长为2,有一个锐角为60°的菱形 ,沿着较短的对角线
,沿着较短的对角线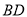 对折,使得
对折,使得
 ,
,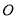 为
为 的中点.
的中点.

(Ⅰ)求证: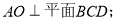
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)求二面角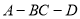 的余弦值.
的余弦值.
(1)见解析;(2)1;(3)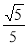
【解析】
试题分析:(1)利用线面垂直的判断定理证明线面垂直,条件齐全.(2)利用棱锥的体积公式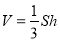 求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.(5)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.(5)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(Ⅰ)连接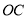 ,由已知得
,由已知得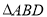 和
和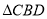 是等边三角形,
是等边三角形,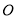 为
为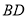 的中点,
的中点,
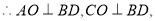 又边长为2,
又边长为2,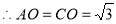
由于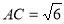 ,在
,在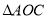 中,
中,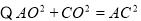
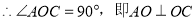
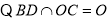 ,
,
(Ⅱ)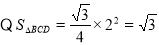 ,
,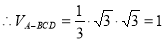

(Ⅲ)解法一:过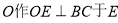 ,连接AE,
,连接AE,
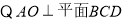 ,
,
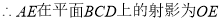

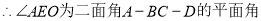
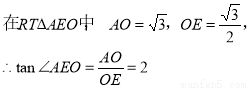
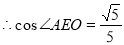
即二面角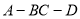 的余弦值为
的余弦值为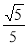 .
.
解法二:以O为原点,如图建立空间直角坐标系,则
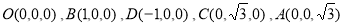
显然,平面 的法向量为
的法向量为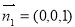

设:平面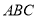 的法向量
的法向量 ,
,
由 ,
, ,
,
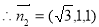

∴二面角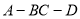 的余弦值为
的余弦值为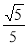 .
.
考点:(1)空间中线面垂直的判定;(2)三棱锥的体积公式;(3)利用空间向量证明线线垂直和求夹角.


科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
已知双曲线 的右焦点
的右焦点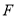 是抛物线
是抛物线 的焦点,两曲线的一个公共
的焦点,两曲线的一个公共
点为 ,且
,且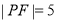 ,则双曲线的离心率为
,则双曲线的离心率为
A. B.
B. C.
C.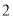 D.
D.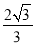
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:填空题
定义:区间[x1,x2](x1<x2)的长度为x2-x1,已知函数y=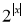 |的定义域为[a,b],值域为[1,2],则区间[a,b]的长度的最大值与最小值的差为________.
|的定义域为[a,b],值域为[1,2],则区间[a,b]的长度的最大值与最小值的差为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com