
分析 (Ⅰ)当a=1时,化简f(x)=|x+1|+|x|.通关当x≥1,当0<x<1,当x≤0,分别求解不等式的解集即可.(Ⅱ)若存在x∈R,使得f(x)<2恒成立,则f(x)在R上最小值应小于2.利用绝对值的几何意义,转化求解即可.
解答 解:(Ⅰ)当a=1时,f(x)=|x+1|+|x|.
当x≥1,得f(x)=2x-1,由f(x)≥2得x≥$\frac{3}{2}$,此时x$≥\frac{3}{2}$;
当0<x<1,得f(x)=1,此时显然f(x)≥2无解;
当x≤0,得f(x)=1-2x,由f(x)≥2得x$≤-\frac{1}{2}$,此时x$≤-\frac{1}{2}$.
综上,不等式f(x)≥2的解集为:$(-∞,-\frac{1}{2}]∪[\frac{3}{2},+∞)$.
(Ⅱ)若存在x∈R,使得f(x)<2恒成立,则f(x)在R上最小值应小于2.
由绝对值不等式得|x-a|+|x|≥|x-a-x|=|a|,则|a|<2,解得-2<a<2,
从而a的取值范围为:(-2,2).
点评 本题考查函数恒成立条件的应用,绝对值不等式的解法,几何意义的应用,考查计算能力.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
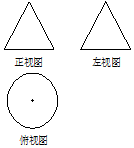 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com