
分析 由题意可得,在[-1,$\frac{1}{2}$]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方,数形结合、分类讨论求得a的范围.
解答  解:函数f(x)=x(1+a|x|)=$\left\{\begin{array}{l}{{ax}^{2}+x,x≥0}\\{{-ax}^{2}+x,x<0}\end{array}\right.$是奇函数,
解:函数f(x)=x(1+a|x|)=$\left\{\begin{array}{l}{{ax}^{2}+x,x≥0}\\{{-ax}^{2}+x,x<0}\end{array}\right.$是奇函数,
关于x的不等式f(x+a)<f(x)的解集 A?[-1,$\frac{1}{2}$],
则在[-1,$\frac{1}{2}$]上,函数y=f(x+a)的图象应在函数y=f(x)
的图象的下方.
当a=0时,显然不满足条件.
当a>0时,如右图所示,函数y=f(x)在R上单调递增,
f(x+a)的图象是把f(x)的图象向左平移a个单位得到的,
不满足在[-1,$\frac{1}{2}$]上,函数y=f(x+a)的图象在
函数y=f(x)的图象下方.
当a<0时,f(x)在($\frac{1}{2a}$,-$\frac{1}{2a}$]上增函数,在(-$\frac{1}{2a}$,+∞)、(-∞,$\frac{1}{2a}$)上是减函数,
要使在[-1,$\frac{1}{2}$]上,函数y=f(x+a)的图象在函数y=f(x)的图象的下方,
如下图所示:
只要f(-1+a)<f(-1)即可,即-a${(-\frac{1}{2}+a)}^{2}$+(-$\frac{1}{2}$+a)<-a${(-\frac{1}{2})}^{2}$-$\frac{1}{2}$,
化简可得 a2-2a-1<0,解得 1-$\sqrt{2}$<a<0,
故答案为:(1-$\sqrt{2}$,0).
点评 本题主要考查分段函数的应用,不等式的解法,体现了转化、数形结合的数学思想,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,已知F1,F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,且|F1F2|=2,若以坐标原点O为圆心,|F1F2|为直径的圆与该双曲线的左支相交于A,B两点,且△F2AB为正三角形,则双曲线的实轴长为$\sqrt{3}$-1.
如图所示,已知F1,F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,且|F1F2|=2,若以坐标原点O为圆心,|F1F2|为直径的圆与该双曲线的左支相交于A,B两点,且△F2AB为正三角形,则双曲线的实轴长为$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
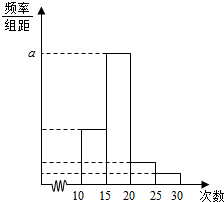 对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:
对某校高一年级学生参加“社区志愿者”活动次数进行统计,随机抽取M名学生作为样本,得到这M个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30] | 1 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com