
| A. | (0,+∞) | B. | $({\frac{{\sqrt{5}-1}}{2},+∞})$ | C. | $({0,\frac{{\sqrt{5}+1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ |
分析 化简可得$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$=$\frac{b}{a}$,设$\frac{b}{a}$=t,由题意可得c=$\frac{{b}^{2}}{a}$,由三边关系可得abc的不等式组,把c=$\frac{{b}^{2}}{a}$代入可得t的不等式组,解不等式组可得.
解答 解:由三角函数公式和正弦定理化简可得:
$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$=$\frac{sinA+cosA•\frac{sinC}{cosC}}{sinB+cosB•\frac{sinC}{cosC}}$
=$\frac{sinAcosC+cosAsinC}{sinBcosC+cosBsinC}$=$\frac{sin(A+C)}{sin(B+C)}$=$\frac{sinB}{sinA}$=$\frac{b}{a}$,
设$\frac{b}{a}$=t,(t>0),由题意可得b2=ac,即c=$\frac{{b}^{2}}{a}$,
代入到a+b>c可得a+b>$\frac{{b}^{2}}{a}$,可得a2+ab>b2,
两边同除以a2可得1+$\frac{b}{a}$>($\frac{b}{a}$)2,即1+t>t2,
整理可得t2-t-1<0,解得$\frac{1-\sqrt{5}}{2}$<t<$\frac{1+\sqrt{5}}{2}$,
同理把c=$\frac{{b}^{2}}{a}$代入a+c>b和b+c>a可解得t<$\frac{-1-\sqrt{5}}{2}$或t>$\frac{\sqrt{5}-1}{2}$
综上可得$\frac{\sqrt{5}-1}{2}$<t<$\frac{1+\sqrt{5}}{2}$,
故选:D.
点评 本题考查两角和与差的三角函数和正弦定理,涉及三角形的三边关系和一元二次不等式的解集,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
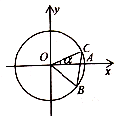 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0<b-1<a<1 | B. | 0<a-1<b<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b-1<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2枝玫瑰的价格高 | B. | 3枝康乃馨的价格高 | ||
| C. | 价格相同 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com