Question

12．如果函数y=f（x）的导函数f′（x）的图象如图所示，给出下列判断：
①函数y=f（x）在区间$（-3，-\frac{1}{2}）$内单调递增；
②函数y=f（x）在区间（4，5）内单调递增；
③函数y=f（x）的最小值是f（-2）和f（4）中较小的一个；
④函数y=xf′（x）在区间（-3，-2）内单调递增；
⑤函数y=xf′（x）在区间$（-\frac{1}{2}，3）$内有极值点；
则上述判断中正确的是②③⑤．

Answer 1

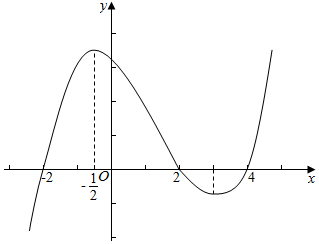
分析 根据函数单调性和导数之间的关系分别判断函数的导数的符号即可得到结论．

解答 解：①函数y=f（x）在区间（-3，-2）上f′（x）＜0，函数为减函数，则①错误；
②函数y=f（x）在区间（4，5）内f′（x）＞0，则函数单调递增；故②正确，
③由图象知当x=-2或4时，函数f（x）取得极小值，则函数y=f（x）的最小值是f（-2）和f（4）中较小的一个，③正确；
④函数y=xf′（x）在区间（-3，-2）的导数为y′=f′（x）+x[f′（x）]′，
∵当-3＜x＜-2时，f′（x）＜0，且f′（x）为增函数，∴[f′（x）]′＞0，
∴y′=f′（x）+x[f′（x）]′＜0，即y=xf'（x）在区间（-3，-2）上单调递减，故④错误，
⑤函数y=xf′（x）的导数y′=f′（x）+x[f′（x）]′，
当-$\frac{1}{2}$＜x＜0时，f′（x）＞0，f′（x）为减函数，∴[f′（x）]′＜0，
此时y′=f′（x）+x[f′（x）]′＞0此时函数y=xf'（x）为增函数，
当2＜x＜3时，f′（x）＜0，f′（x）为减函数，∴[f′（x）]′＜0，
此时y′=f′（x）+x[f′（x）]′＜0此时函数y=xf'（x）为减函数，
则函数y=xf'（x）在区间$（-\frac{1}{2}，3）$内有极值点；故⑤正确，
故答案为：②③⑤．

点评 本题主要考查命题的真假判断，涉及函数单调性和导数，极值和导数之间的关系，考查学生的识图和用图的能力．综合性较强，有一定的难度．