
分析 令f(m)=m(x2-1)-2x+1,由条件f(m)<0对满足|m|≤2的一切m的值都成立,利用一次函数的单调性可得:f(-2)<0,f(2)<0.解出即可.
解答 解:令f(m)=mx2-2x-m+1=m(x2-1)-2x+1,
若对满足|m|≤2的一切m的值不等式恒成立,则只需$\left\{\begin{array}{l}{f(-2)<0}\\{f(2)<0}\end{array}\right.$即可,
所以$\left\{\begin{array}{l}{-2({x}^{2}-1)-2x+1<0}\\{2({x}^{2}-1)-2x+1<0}\end{array}\right.$,解得$\frac{-1+\sqrt{7}}{2}$<x<$\frac{1+\sqrt{3}}{2}$,
所以实数x的取值范围是($\frac{-1+\sqrt{7}}{2}$,$\frac{1+\sqrt{3}}{2}$).
点评 本题以不等式为载体,考查恒成立问题,解题的关键是等价转化,构造新函数,属于基础题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 以4为首项,3为公比的等比数列 | B. | 以4为首项,$\frac{1}{3}$为公比的等比数列 | ||
| C. | 以$\frac{4}{3}$为首项,3为公比的等比数列 | D. | 以$\frac{4}{3}$为首项,$\frac{1}{3}$为公比的等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
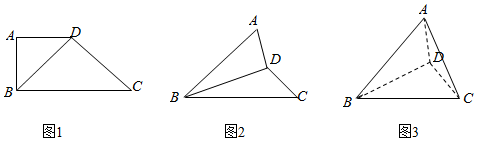
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
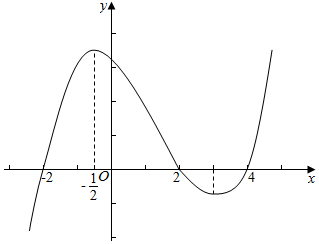
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A. | -10 | B. | -8 | C. | -6 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com