Question

5．在梯形ABCD中，AD∥BC，BC=2AD，AB=AD=$\sqrt{2}$，AB⊥BC，如图把△ABD沿BD翻折，使得平面ABD⊥平面BCD

（1）求证：CD⊥平面ABD；
（2）若M为线段BC中点，求三棱锥M-ACD的体积．

Answer 1

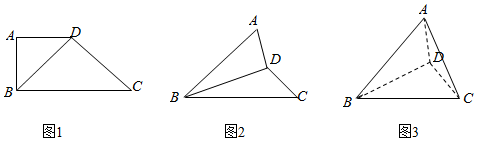
分析 （1）过D作DE⊥BC，利用勾股定理求出BD，CD，根据勾股定理的逆定理证明BD⊥CD，利用面面垂直的性质得出CD⊥平面ABD；
（2）由于M为BC的中点，故三棱锥M-ACD的体积为三棱锥B-ACD的体积的一半．

解答 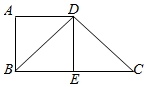证明：（1）过D作DE⊥BC，
∵AB=AD，AD∥BC，AB⊥BC，
∴四边形ABED是正方形，
∴DE=AB=$\sqrt{2}$，BE=AD=$\sqrt{2}$，BD=$\sqrt{2}$AB=2．
∵BC=2AD=2$\sqrt{2}$，∴CE=$\sqrt{2}$，
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}=2$．
∴BD²+CD²=BC²，∴BD⊥CD．
∵平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，CD?平面BCD，
∴CD⊥平面ABD．
（2）V_B-ACD=V_C-ABD=$\frac{1}{3}{S}_{△ABD}•CD$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×2$=$\frac{2}{3}$．
∵M是BC的中点，
∴V_M-ACD=$\frac{1}{2}{V}_{B-ACD}$=$\frac{1}{3}$．

点评 本题考查了侧面垂直的判定，棱锥的体积计算，属于中档题．