
| A. | $\frac{5}{3}或\frac{4}{3}$ | B. | $\frac{{4\sqrt{7}}}{7}或\frac{4}{3}$ | C. | $\frac{{4\sqrt{7}}}{7}$ | D. | $\frac{4}{3}$ |
分析 由条件根据渐近线方程,分类讨论,求得双曲线C的离心率的值.
解答 解:当焦点在x轴上时,由题意可得$\frac{b}{a}$=$\frac{\sqrt{7}}{3}$,设a=3k,b=$\sqrt{7}$k,∴c=$\sqrt{{a}^{2}{+b}^{2}}$=4k,
∴$\frac{c}{a}$=$\frac{4}{3}$.
当焦点在y轴上时,由题意可得$\frac{a}{b}$=$\frac{\sqrt{7}}{3}$,设b=3k,a=$\sqrt{7}$k,∴c=$\sqrt{{a}^{2}{+b}^{2}}$=4k,
∴$\frac{c}{a}$=$\frac{4}{\sqrt{7}}$=$\frac{4\sqrt{7}}{7}$.
综上可得,双曲线C的离心率为$\frac{4}{3}$或$\frac{4\sqrt{7}}{7}$,
故选:B.
点评 本题主要考查双曲线的简单性质的应用,属于基础题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
 如图,已知线段AB长度为a(a为定值),在其上任意选取一点M,在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF,⊙P和⊙Q是这两个正方形的外接圆,它们交于点M、N.试以A为坐标原点,建立适当的平面直角坐标系.
如图,已知线段AB长度为a(a为定值),在其上任意选取一点M,在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF,⊙P和⊙Q是这两个正方形的外接圆,它们交于点M、N.试以A为坐标原点,建立适当的平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 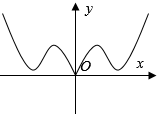 | ||
| C. |  | D. | 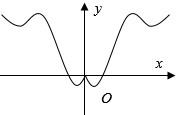 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (-2,0) | C. | $(0,-\frac{1}{8})$ | D. | $(0,-\frac{1}{16})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com