
分析 由an=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$(n≥2,n∈N*),an+1=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$+$\frac{1}{n}$an,(n≥2,n∈N*),两式相减整理得:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,累乘即可求得an=n,即可求得k的值.
解答 解:根据题意得,an=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$(n≥2,n∈N*),
an+1=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$+$\frac{1}{n}$an,(n≥2,n∈N*),
∴an+1=an+$\frac{1}{n}$an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
an=2×$\frac{3}{2}$×…×$\frac{n}{n-1}$=n,(n≥2,n∈N*),
∴an=n,
由ak=2017,则k=2017,
故答案为:2017.
点评 本题考查数列的递推公式,考查数列通项公式的求法,考查计算能力,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,e4) | C. | (e4,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2,\frac{5π}{6})$ | B. | $(2,\frac{7π}{6})$ | C. | $(2,\frac{11π}{6})$ | D. | $(2,\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
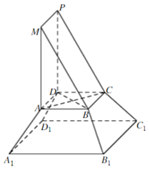 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.
《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
| A. | 05 | B. | 09 | C. | 07 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com