
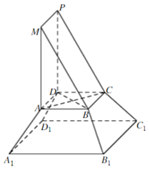
 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.
《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.分析 (Ⅰ)证明AD⊥MA,推出MA⊥平面ABCD,得到MA⊥BD.结合BD⊥AC,证明BD⊥平面MAC.
(Ⅱ)设刍童ABCD-A1B1C1D1的高为h,利用几何体的体积公式,转化求解即可.
解答 解:(Ⅰ)证明:由题可知ABM-DCP是底面为直角三角形的直棱柱,
∴AD⊥平面MAB,
又MA?平面MAB,∴AD⊥MA,
又MA⊥AB,AD∩AB=A,AD,AB?平面ABCD,
∴MA⊥平面ABCD,
又BD?平面ABCD,
∴MA⊥BD.
又AB=AD,∴四边形ABCD为正方形,
∴BD⊥AC,
又MA∩AC=A,MA,AC?平面MAC,
∴BD⊥平面MAC.…(6分)
(Ⅱ)设刍童ABCD-A1B1C1D1的高为h,
则三棱锥A-A1B1D1体积V=$\frac{1}{3}×\frac{1}{2}×2×2×h$=$\frac{2\sqrt{3}}{3}$,
∴h=$\sqrt{3}$,
故该组合体的体积为V=$\frac{1}{2}×1×\sqrt{3}×1+\frac{1}{3}({1}^{2}+{2}^{2}+\sqrt{{1}^{2}+{2}^{2}})×\sqrt{3}$=$\frac{17\sqrt{3}}{6}$.
点评 本题考查直线与平面垂直的判定定理的应用,组合体的体积的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | a,b都为偶数 | B. | a,b不为偶数 | ||
| C. | a,b都不为偶数 | D. | a,b中有一个不为偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 4π | C. | 9π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{2π}{3}$ | $\frac{8π}{3}$ | |||
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com