
| A. | π | B. | 4π | C. | 9π | D. | 16π |
分析 设点A(a,b),则点A得到直线xcosθ+ysinθ=4+$\sqrt{2}$sin(θ+$\frac{π}{4}$)的距离为d,根据点到直线的距离公式求出当a=1,b=1时,d=4,根据直线与圆相切时,圆心到直线的距离等于半径得到直线组xcosθ+ysinθ=4+$\sqrt{2}$sin(θ+$\frac{π}{4}$)所围成的图形是以(1,1)为圆心,以4为半径的圆,则答案可求.
解答 解:设点A(a,b),则点A得到直线xcosθ+ysinθ=4+$\sqrt{2}$sin(θ+$\frac{π}{4}$)的距离为d,
则d=$\frac{|(a-1)cosθ+(b-1)sinθ-4|}{\sqrt{si{n}^{2}θ+co{s}^{2}θ}}$,当a=1,b=1时,d=4,根据直线与圆相切时,圆心到直线的距离等于半径得:
直线组xcosθ+ysinθ=4+$\sqrt{2}$sin(θ+$\frac{π}{4}$)所围成的图形是以(1,1)为圆心,以4为半径的圆,其面积为16π.
故选:D.
点评 本题考查直线系方程的应用,考查数学转化思想方法,考查推理能力与计算能力,属中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
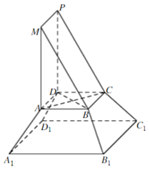 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.
《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
| A. | 05 | B. | 09 | C. | 07 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ac2>bc2 | C. | 2-a<2-b | D. | lga>lgb |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com