=\left\{\begin{array}{l}x.x＜1\\{x^3}-\frac{1}{x}+1.x≥1\end{array}\right.$.则$f$=$\frac{2}{17}$．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

4．（文科）设函数$f（x）=\left\{\begin{array}{l}x，x＜1\\{x^3}-\frac{1}{x}+1，x≥1\end{array}\right.$，则$f（\frac{1}{f（2）}）$=$\frac{2}{17}$．

分析利用分段函数的表达式，逐步求解函数值即可．

解答解：设函数$f（x）=\left\{\begin{array}{l}x，x＜1\\{x^3}-\frac{1}{x}+1，x≥1\end{array}\right.$，
则f（2）=8-$\frac{1}{2}+1$=$\frac{17}{2}$．
$f（\frac{1}{f（2）}）$=f（$\frac{2}{17}$）=$\frac{2}{17}$．
故答案为：$\frac{2}{17}$．

点评本题考查分段函数的应用，函数值的求法，考查计算能力．

练习册系列答案

火辣英语初中阅读理解与完形填空系列答案

交大之星现代文经典阅读300题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

14．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，若直线l的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y={y}_{0}+tsinα}\end{array}\right.$（t为参数，α为l的倾斜角），曲线E的极坐标方程为ρ=4sinθ．射线θ=β，θ=β+$\frac{π}{4}$，θ=β-$\frac{π}{4}$与曲线E分别交于不同于极点的三点A、B、C．
（1）求证：|OB|+|OC|=$\sqrt{2}$|OA|；
（2）当β=$\frac{7π}{12}$时，直线l过B、C两点，求y₀与α的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．

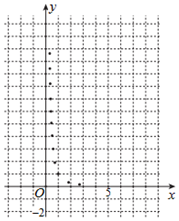某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据，且作了一定的数据处理（如表），得到了散点图（如图）．

$\bar x$	$\bar y$	$\bar w$	$\sum_{i=1}^{10}{（{x_i}-\bar x）^2}$	$\sum_{i=1}^{10}{（{w_i}-\bar w）^2}$	$\sum_{i=1}^{10}（{x_i}-\bar x）（{y_i}-\bar y）$	$\sum_{i=1}^{10}（{w_i}-\bar w）（{y_i}-\bar y）$
1.47	20.6	0.78	2.35	0.81	-19.3	16.2

表中${w_i}=\frac{1}{x_i^2}，\overline{w}=\frac{1}{10}\sum_{i=1}^{10}{w_i}$．
（1）根据散点图判断，y=a+bx与$y=c+\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立y关于x的回归方程；
（3）若旋转的弧度数x与单位时间内煤气输出量t成正比，那么x为多少时，烧开一壶水最省煤气？
附：对于一组数据（u₁，v₁），（u₂，v₂），（u₃，v₃），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\hat β=\frac{{\sum_{i=1}^n{（{v_i}-\bar v）（{u_i}-\bar u）}}}{{\sum_{i=1}^n{{{（{u_i}-\bar u）}^2}}}}，\hat α=\bar v-\hat β\bar u$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．在锐角△ABC中，角A，B，C所对的边分别为a，b，c，且$\overrightarrow{m}$=（$\sqrt{3}$，2sinA），$\overrightarrow{n}$=（c，a）若$\overrightarrow{m}∥\overrightarrow{n}$
（Ⅰ）求角C的大小；
（Ⅱ）若c=$\sqrt{7}$，且△ABC的面积为$\frac{3\sqrt{3}}{2}$，求a+b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．

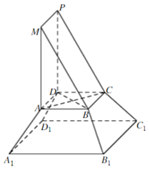《九章算术》是我国古代内容极为丰富的数学名著，书中将底面为直角三角形，且侧棱与底面垂直的棱柱称为堑堵，将底面为矩形的棱台称为刍童．在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD，A₁B₁=A₁D₁．棱台体积公式：V=$\frac{1}{3}$（S′+$\sqrt{S′S}$+S）h，其中S′，S分别为棱台上、下底面面积，h为棱台高．
（Ⅰ）证明：直线BD⊥平面MAC；
（Ⅱ）若AB=1，A₁D₁=2，MA=$\sqrt{3}$，三棱锥A-A₁B₁D₁的体积V=$\frac{2\sqrt{3}}{3}$，求该组合体的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．设f（x）=xln x-ax²+（2a-1）x，a∈R．
（1）令g（x）=f′（x），求g（x）的单调区间；
（2）已知f（x）在x=1处取得极大值，求正实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．若复数$\frac{2+ai}{1-i}（{a∈R}）$是纯虚数（i是虚数单位），则复数z=a+（a-3）i在复平面内对应的点位于第四象限．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．设a，b∈R，若a＞b，则（　　）

A．

$\frac{1}{a}＜\frac{1}{b}$

B．