考点:二面角的平面角及求法,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件,推导出A1D⊥AD1,A1D⊥AE,由此能够证明AD1⊥面AD1E,从而得到A1D⊥D1E.
(Ⅱ)连结DE,由已知条件推导出∠DFD1是二面角D-CE-D1的平面角,由此能求出二面角D-CE-D1的平面角的正切值.
解答:
(Ⅰ)证明:在长方体ABCD-A
1B
1C
1D
1中,
∵AD=AA
1=1,∴A
1D⊥AD
1,
又在长方体ABCD-A
1B
1C
1D
1中,
∵AB⊥侧面ADD
1A
1,A
1D?侧面ADD
1A
1,
∴A
1D⊥AB,即A
1D⊥AE,
又∵AD
1∩AE=A,AD
1,AE?面AD
1E,
∴AD
1⊥面AD
1E,∴A
1D⊥D
1E.(6分)
(Ⅱ)解:连结DE,在矩形ABCD中,
∵AB=2,AD=1,且E为AB中点,∴DE⊥CE,且DE=
,
又∵DD
1⊥底面ABCD,CE?底面ABCD,
∴DD
1⊥CE,而DD
1∩DE=D,DD
1,DE?面DD
1E,
∴CE⊥面DD
1E,D
1E?面DD
1E,∴D
1E⊥CE,
∴∠DFD
1是二面角D-CE-D
1的平面角,
在Rt△DD
1E中,tan∠DED
1=
=
=
,
∴二面角D-CE-D
1的平面角的正切值为
.(6分)
点评:本题考查异面直线垂直的证明,考查二面角的正切值的求法,解题时要注意空间思维能力的培养,合理地化空间问题为平面问题.

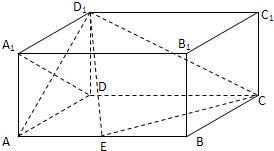 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案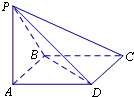 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且PC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且PC=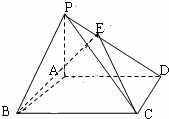 (理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.
(理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.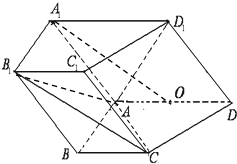 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= 已知椭圆
已知椭圆