
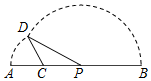
 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3. 分析 本题要根据实际情况计算出定义域与函数的零点,可以看出所给的条件是△CPD,故可根据其是三角形求出自变量的范围.面积表达式可以用海伦公式求出,对所得的函数求导,令导数为0,解出即可.
解答 解:由题意,DC=2,CP=x,DP=6-x
∵△CPD,∴$\left\{\begin{array}{l}{2+x>6-x}\\{2+6-x>x}\\{x+6-x>2}\end{array}\right.$,解得x∈(2,4)
如图,三角形的周长是一个定值8,
故其面积可用海伦公式表示出来即f(x)=$\sqrt{4×(4-x)×(4-6+x)×2}$=$\sqrt{-{8x}^{2}+48x-64}$,
∴f′(x)=$\frac{-16x+48}{\sqrt{-{8x}^{2}+48x-64}}$,
令 f′(x)=0,解得x=3,
故答案为:(2,4),3.
点评 本题考查根据实际问题选择函数类型,本题中求函数解析式用到了海伦公式,学习中积累一些知识储备,视野开阔,易找出简单的解题方法.本题考查到了复合函数求导公式,有一定的综合性.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都表示一条直线和一个圆 | |
| B. | 都表示两个点 | |
| C. | 前者是两个点,后者是一直线和一个圆 | |
| D. | 前者是一条直线和一个圆,后者是两个点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{4}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{3\sqrt{5}}}{10}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某次运动会甲、乙两名射击运动员的成绩如下:
某次运动会甲、乙两名射击运动员的成绩如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com