考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离
分析:①可通过BC1∥平面AD1C,则BC1上任一点到平面AD1C的距离相等,VA-D1PC=VP-AD1C,即可判断;
②可通过BC1∥平面AD1C,则BC1上任一点到平面AD1C的距离相等,即可判断;
③由线面垂直的判定和性质,即可得到;
④由面面平行的判定,即可得证;
⑤由于在空间中与点C1和D距离相等点在垂直且平分线段DC1的平面上,即平面A1BCD1,又平面A1BCD1∩平面A1B1C1D1=A1D1,即可得到.
解答:
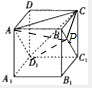
解:①∵BC
1∥AD
1,∴BC
1∥平面AD
1C,∴BC
1上任一点到平面AD
1C的距离相等,
又V
A-D1PC=V
P-AD1C,则三棱锥A-D
1PC的体积不变,故①正确;
②点P在直线BC
1,从B到C
1上运动时,AP的长度会改变,但P到平面AD
1C的距离不变,
故②错;
③∵A
1D⊥平面ABC
1D
1,AP?平面ABC
1D
1,∴A
1D⊥AP,故③正确;
④∵平面AD
1C∥平面A
1BC
1,∴平面AD
1C∥平面A
1BP,故④正确;
⑤由于在空间中与点C
1和D距离相等点在垂直且平分线段DC
1的平面上,即平面A
1BCD
1,又平面
A
1BCD
1∩平面A
1B
1C
1D
1=A
1D
1,∴平面A
1B
1C
1D
1上与点D和C
1距离相等点的轨迹是过D
1点的直线
故⑤正确.
故答案为:①③④⑤
点评:本题考查空间位置关系和距离和体积,考查线面的位置关系和面面的位置关系,主要是垂直和平行,记熟这些定理是迅速解题的关键.

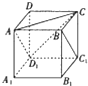 如图,正方体ABCD-A1B1C1D1,则下列五个命题:
如图,正方体ABCD-A1B1C1D1,则下列五个命题: 解:①∵BC1∥AD1,∴BC1∥平面AD1C,∴BC1上任一点到平面AD1C的距离相等,
解:①∵BC1∥AD1,∴BC1∥平面AD1C,∴BC1上任一点到平面AD1C的距离相等,
