
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点;当直线
两点;当直线![]() 经过椭圆
经过椭圆![]() 的下顶点
的下顶点![]() 和右焦点
和右焦点![]() 时,
时,![]() 的周长为
的周长为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 为
为![]() 内一点,
内一点,![]() 为坐标原点,满足
为坐标原点,满足![]() ,若点
,若点![]() 恰好在圆
恰好在圆![]() 上,求实数
上,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】一个盒子里装有![]() 个均匀的红球和
个均匀的红球和![]() 个均匀的白球,每个球被取到的概率相等,已知从盒子里一次随机取出1个球,取到的球是红球的概率为
个均匀的白球,每个球被取到的概率相等,已知从盒子里一次随机取出1个球,取到的球是红球的概率为![]() ,从盒子里一次随机取出2个球,取到的球至少有1个是白球的概率为
,从盒子里一次随机取出2个球,取到的球至少有1个是白球的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若一次从盒子里随机取出3个球,求取到的白球个数不小于红球个数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
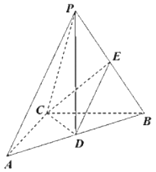
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为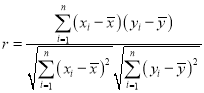 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中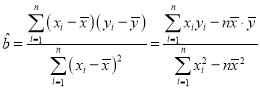 ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)当![]() 时,直线
时,直线![]() 被圆
被圆![]() 截得的弦长为__________;
截得的弦长为__________;
(2)若在圆![]() 上存在一点
上存在一点![]() ,在直线
,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 的中点恰为坐标原点
的中点恰为坐标原点![]() ,则实数
,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:其中正确命题数是( )
A.在线性回归模型中,相关系数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 变化的贡献率,
变化的贡献率,![]() 越接近于1,表示回归效果越好
越接近于1,表示回归效果越好
B.两个变量相关性越强,则相关系数的绝对值就越接近于1
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位
平均减少0.5个单位
D.对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值来说,观测值越小,“
的观测值来说,观测值越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com