
分析 由第三步可知,n表示y=4x2下方的点A的个数,其概率为$\frac{n}{M}$=$\frac{51}{150}$,故点落在y=4x2上方的概率为1-$\frac{n}{M}$=1-$\frac{51}{150}$=$\frac{33}{50}$;先由计算器做模拟试验结果试验估计,得出点落在阴影部分的点的概率,再转化为几何概型的面积类型求解区域Ω的面积S.
解答 解:由第三步可知,n表示y=4x2下方的点A的个数,其概率为$\frac{n}{M}$=$\frac{51}{150}$,故点落在y=4x2上方的概率为1-$\frac{n}{M}$=1-$\frac{51}{150}$=$\frac{33}{50}$;
矩形的面积为4×2=8,
设区域Ω的面积为S,则有$\frac{S}{8}$=$\frac{33}{50}$,
∴S=$\frac{33}{50}$×8=$\frac{132}{25}$.
故答案为:$\frac{132}{25}$.
点评 本题考查模拟方法估计概率以及几何概型中面积类型,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
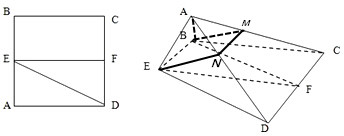 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线y=g(x)的一个对称中心为点(-$\frac{π}{12}$,0) | |
| B. | 曲线y=g(x)的一个对称轴为直线x=$\frac{kπ}{4}$+$\frac{π}{16}$(k∈Z) | |
| C. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减 | |
| D. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内不单调 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com