
| A. | 曲线y=g(x)的一个对称中心为点(-$\frac{π}{12}$,0) | |
| B. | 曲线y=g(x)的一个对称轴为直线x=$\frac{kπ}{4}$+$\frac{π}{16}$(k∈Z) | |
| C. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减 | |
| D. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内不单调 |
分析 利用两角和的正弦化积,由函数的对称中心的纵坐标为-1判断A错误;求出函数的对称轴方程说明B错误;由x∈[$\frac{2π}{3}$,$\frac{3π}{4}$],求得相位的范围,结合正弦函数的单调性说明C正确,D错误.
解答 解:g(x)=sin4x+$\sqrt{3}$cos4x-1=$2sin(4x+\frac{π}{3})-1$,
其对称中心的纵坐标为-1,故A错误;
由$4x+\frac{π}{3}=\frac{π}{2}+kπ$,得$x=\frac{π}{24}+\frac{kπ}{4},k∈Z$,故B错误;
当$\frac{2π}{3}≤x≤\frac{3π}{4}$时,有$\frac{8π}{3}≤4x≤3π$,则$3π≤4x+\frac{π}{3}≤\frac{10π}{3}$,函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减,故C正确,D不正确.
故选:C.
点评 本题考查三角函数中的恒等变换应用,考查了y=Asin(ωx+φ)型函数的图象和性质,是基础题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
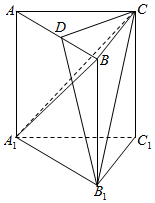 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com