
分析 利用降幂公式化简.
(Ⅰ)由相位在正弦函数的减区间内列式求得x的范围,则y=f(x)的单调减区间可求,再由相位的终边落在y轴上求得x值,可得函数的对称轴方程;
(Ⅱ)求出原函数的增区间,可得y=f(x)在[0,$\frac{1}{3}$]上单调递增,在[$\frac{1}{3},\frac{1}{2}$]上单调递减,再求出f(0)、f($\frac{1}{3}$)、f($\frac{1}{2}$)的值,则可求得满足函数y=f(x)-m在区间[0,$\frac{1}{2}$]上恰好有两个零点的实数m的取值范围.
解答 解:f(x)=$\frac{1}{4}$sin(πx-$\frac{π}{4}$)cos(πx-$\frac{π}{4}$)+$\frac{\sqrt{3}}{4}$cos2(πx-$\frac{π}{4}$)-$\frac{\sqrt{3}}{8}$
=$\frac{1}{8}sin(2πx-\frac{π}{2})+\frac{\sqrt{3}}{4}•\frac{1+cos(2πx-\frac{π}{2})}{2}-\frac{\sqrt{3}}{8}$=$-\frac{1}{8}cos2πx+\frac{\sqrt{3}}{8}sin2πx$=$\frac{1}{4}sin(2πx-\frac{π}{6})$.
(Ⅰ)由$\frac{π}{2}+2kπ≤2πx-\frac{π}{6}≤\frac{3π}{2}+2kπ$,解得$k+\frac{1}{3}≤x≤k+\frac{5}{6}$,k∈Z.
∴y=f(x)的单调减区间为[$k+\frac{1}{3},k+\frac{5}{6}$],k∈Z;
由$2πx-\frac{π}{6}=kπ+\frac{π}{2}$,得$x=\frac{1}{3}+\frac{k}{2}$,k∈Z.
∴y=f(x)的对称轴方程为$x=\frac{1}{3}+\frac{k}{2}$,k∈Z;
(Ⅱ)由$-\frac{π}{2}+2kπ≤2πx-\frac{π}{6}≤\frac{π}{2}+2kπ$,解得$k-\frac{1}{6}≤x≤k+\frac{1}{3}$,k∈Z,
∴y=f(x)在[0,$\frac{1}{3}$]上单调递增,在[$\frac{1}{3},\frac{1}{2}$]上单调递减,
而f(0)=$\frac{1}{4}sin(-\frac{π}{6})=-\frac{1}{8}$,f($\frac{1}{3}$)=$\frac{1}{4}sin\frac{π}{2}=\frac{1}{4}$,f($\frac{1}{2}$)=$\frac{1}{4}sin\frac{5π}{6}=\frac{1}{8}$,
∴若函数y=f(x)-m在区间[0,$\frac{1}{2}$]上恰好有两个零点,即y=f(x)的图象与直线y=m有两个交点,
则实数m的取值范围是[$\frac{1}{8},\frac{1}{4}$).
点评 本题考查三角函数中的恒等变换应用,考查了y=Asin(ωx+φ)型函数的图象和性质,考查计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
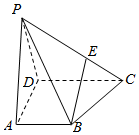 如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.
如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线y=g(x)的一个对称中心为点(-$\frac{π}{12}$,0) | |
| B. | 曲线y=g(x)的一个对称轴为直线x=$\frac{kπ}{4}$+$\frac{π}{16}$(k∈Z) | |
| C. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减 | |
| D. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内不单调 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com