
分析 可写出an=$\frac{5}{9}$(10n-1),从而利用拆项法求其前n项和即可.
解答 解:∵999…9=10n-1,
∴an=$\frac{5}{9}$(10n-1),
故数列5,55,555,…的前n项和为
$\frac{5}{9}$(10-1)+$\frac{5}{9}$(102-1)+$\frac{5}{9}$(103-1)+$\frac{5}{9}$(104-1)+…+$\frac{5}{9}$(10n-1)
=$\frac{5}{9}$(10+102+103+104+…+10n-n)
=$\frac{5}{9}$($\frac{10(1-1{0}^{n})}{1-10}$-n)
=$\frac{5}{9}$($\frac{10(1{0}^{n}-1)}{9}$-n).
点评 本题考查了学生的归纳猜想能力及拆项求和法的应用.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
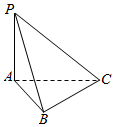 如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.
如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x-1≥0 | B. | ?x∈R,x2-x-1<0 | C. | ?x∈R,x2-x-1>0 | D. | ?x∈R,x2-x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | m | 1 | n | 1 |
| 女 | 1 | 1 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com