
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 先画出图象、做出辅助线,设|AF|=a、|BF|=b,由抛物线定义得2|MN|=a+b,由题意和余弦定理可得|AB|2=a2+b2-2abcosα,再根据$\frac{|AB|}{|MN|}$的最小值为1,即可得到答案.
解答 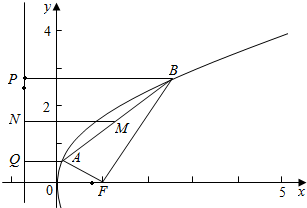 解:如右图:过A、B分别作准线的垂线AQ、BP,垂足分别是Q、P,
解:如右图:过A、B分别作准线的垂线AQ、BP,垂足分别是Q、P,
设|AF|=a,|BF|=b,连接AF、BF,
由抛物线定义,得|AF|=|AQ|,|BF|=|BP|
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2-2abcosα,
∵$\frac{|AB|}{|MN|}$的最小值为1,
∴a2+b2-2abcosα≥$\frac{(a+b)^{2}}{4}$,α=$\frac{π}{3}$时,不等式恒成立.
故选:C.
点评 本题考查抛物线的定义、简单几何性质,基本不等式求最值,余弦定理的应用等知识,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2α+β=$\frac{π}{2}$ | B. | 2α-β=$\frac{π}{2}$ | C. | α+2β=$\frac{π}{2}$ | D. | α-2β=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{5}$ | C. | -$\frac{5\sqrt{3}}{3}$ | D. | -$\frac{3\sqrt{3}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
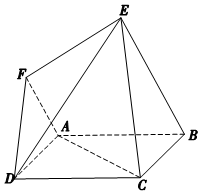 如图,正方形ABCD的边长等于2,平面ABCD⊥平面ABEF,AF∥BE,BE=2AF=2,EF=$\sqrt{3}$.
如图,正方形ABCD的边长等于2,平面ABCD⊥平面ABEF,AF∥BE,BE=2AF=2,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )
如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $1-\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com