
| A. | P1∧(¬P2) | B. | (¬P1)∧P2 | C. | (¬P1)∧¬P2 | D. | P1∧P2 |
分析 分别求出命题P1、命题P2的真假,从而求出复合命题的真假即可.
解答 解:令x2=-x1,不等式|f(x1)-f(x2)|≥|g(x1)-g(x2)|恒成立,
∴不等式|f(x1)-f(-x1)|≥|g(x1)-g(-x1)|恒成立,
∵f(x)是偶函数,∴f(-x1)=f(x1),
∴f(x1)-f(-x1)=0,
∴不等式0≥|g(x1)-g(-x1)|恒成立,又|g(x1)-g(-x1)|≥0,
∴g(x1)-g(-x1)=0,∴g(-x1)=g(x1),
∴函数g(x)是偶函数,故命题命题P1是真命题;
若x≠0时,x•f′(x)>0在R上恒成立,
则f(x)在(-∞,0)递减,在(0,+∞)递增,
∵|f(x1)-f(x2)|>|g(x1)-g(x2)|恒成立,
设x1<x2,x>0时,
∴f(x1)-f(x2)<g(x1)-g(x2)<f(x2)-f(x1),
∴h(x1)-h(x2)=f(x1)-f(x2)+g(x1)-g(x2)<f(x1)-f(x2)+f(x2)-f(x1),
∴h(x1)-h(x2)<0,
x<0时,h(x1)-h(x2)>0,
∴函数h(x)=f(x)+g(x)在(-∞,0)递减,在(0,+∞)上是增函数,
故命题P2是假命题;
故选:A.
点评 本题考查函数的周期性、奇偶性,考查复合命题的判断,考查学生分析解决问题的能力,属于中档题


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
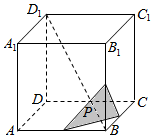 如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )
如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 108 | C. | 180 | D. | 216 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在PD、PC上,2PN=NC,PM=MD
如图,已四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在PD、PC上,2PN=NC,PM=MD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
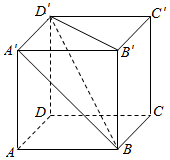 如图所示,在棱长为2的正方体ABCD-A′B′C′D′中,求:
如图所示,在棱长为2的正方体ABCD-A′B′C′D′中,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 是非奇非偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com