
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x>y>z | B. | z>y>x | C. | y>x>z | D. | z>x>y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (2,3) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:解答题
某中学的高二(1)班男同学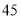 名,女同学
名,女同学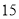 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个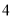 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出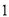 名同学做实验,该同学做完后,再从小组内剩下的同学中选
名同学做实验,该同学做完后,再从小组内剩下的同学中选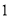 名同学做实验,求选出的两名同学中恰有
名同学做实验,求选出的两名同学中恰有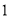 名女同学的概率;
名女同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为 ,第二次做实验的同学得到的实验数据为
,第二次做实验的同学得到的实验数据为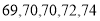 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,如果输入的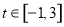 ,则输出的s属于( )
,则输出的s属于( )
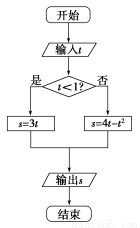
A.[-3,4] B.[-5,2] C.[-4,3] D.[-2,5]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com