
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
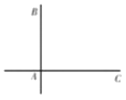
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.![]() 分别为
分别为![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点.
的中点.
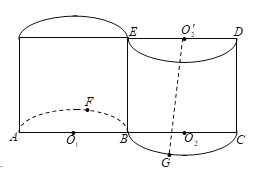
(1)求直线![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆C上,直线l过
在椭圆C上,直线l过![]() 交椭圆于A,B两点.
交椭圆于A,B两点.
(1)求椭圆C的标准方程;
(2)当![]() 时,点A在x轴上方时,求点A,B的坐标;
时,点A在x轴上方时,求点A,B的坐标;
(3)若直线![]() 交y轴于点M,直线
交y轴于点M,直线![]() 交y轴于点N,是否存在直线l,使得
交y轴于点N,是否存在直线l,使得![]() 与
与![]() 的面积满足
的面积满足![]() ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,其内接正方形的面积为4.
,其内接正方形的面积为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设M为椭圆C的右顶点,过点![]() 且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]() .
.
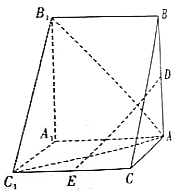
(1)证明:![]() 是
是![]() 的中点;
的中点;
(2)设![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为30°,求两面角
所成的角为30°,求两面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),把曲线
为参数),把曲线![]() 横坐标缩短为原来的
横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() ,直线
,直线![]() 的普通方程是
的普通方程是![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系;
轴正半轴为极轴建立极坐标系;
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市开展年终大回馈,设计了两种答题游戏方案:
方案一:顾客先回答一道多选题,从第二道开始都回答单选题;
方案二:顾客全部选择单选题进行回答;
其中每道单选题答对得2分,每道多选题答对得3分,无论单选题还是多选题答错都得0分,每名参与的顾客至多答题3道.在答题过程中得到3分或3分以上立刻停止答题,并获得超市回馈的赠品.
为了调查顾客对方案的选择情况,研究人员调查了参与游戏的500名顾客,所得结果如下表所示:
男性 | 女性 | |
选择方案一 | 150 | 80 |
选择方案二 | 150 | 120 |
(1)是否有95%的把握认为方案的选择与性别有关?
(2)小明回答每道单选题的正确率为0.8,多选题的正确率为0.75,.
①若小明选择方案一,记小明的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
②如果你是小明,你觉得选择哪种方案更有可能获得赠品,请通过计算说明理由.
附:![]() ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空有限集合![]() 是由若干个正实数组成,集合
是由若干个正实数组成,集合![]() 的元素个数
的元素个数![]() .对于任意
.对于任意![]() ,数
,数![]() 或
或![]() 中至少有一个属于
中至少有一个属于![]() ,称集合
,称集合![]() 是“好集”:否则,称集合
是“好集”:否则,称集合![]() 是“坏集”.
是“坏集”.
(1)判断![]() 和
和![]() 是“好集”,还是“坏集”;
是“好集”,还是“坏集”;
(2)题设的有限集合![]() 中,既有大于1的元素,又有小于1的元素,证明:集合
中,既有大于1的元素,又有小于1的元素,证明:集合![]() 是“坏集”.
是“坏集”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com