
分析 (Ⅰ)求出f'(x)=lnx+1,推出单调区间,然后求解函数的最小值.
(Ⅱ)存在${x_0}∈[{\frac{1}{e},e}]$使得mf'(x)+g(x)≥2x+m成立,转化为存在${x_0}∈[{\frac{1}{e},e}]$使得$m≤{(\frac{{2x-{x^2}}}{lnx-x})_{max}}$成立,令$k(x)=\frac{{2x-{x^2}}}{lnx-x}$,$x∈[{\frac{1}{e},e}]$,则$k'(x)=\frac{(x-1)(2lnx+x+2)}{{{{(lnx-x)}^2}}}$,通过判断导函数的符号,求出最大值,
解答 解:(Ⅰ)f'(x)=lnx+1,
令f'(x)>0,解得$x>\frac{1}{e}$;令f'(x)<0,解得$0<x<\frac{1}{e}$,
∴f(x)在$(0,\frac{1}{e})$递减,在$(\frac{1}{e},+∞)$递增,
若$t≥\frac{1}{e}$,则f(x)在[t,t+2]递增,
∴f(x)min=f(t)=tlnt+2;
若$0<t<\frac{1}{e}$,则f(x)在$[t,\frac{1}{e})$递减,在$(\frac{1}{e},t+2]$递增,
∴$f{(x)_{min}}=f(\frac{1}{e})=2-\frac{1}{e}$.
(Ⅱ)若存在${x_0}∈[{\frac{1}{e},e}]$使得mf'(x)+g(x)≥2x+m成立,
即存在${x_0}∈[{\frac{1}{e},e}]$使得$m≤{(\frac{{2x-{x^2}}}{lnx-x})_{max}}$成立,
令$k(x)=\frac{{2x-{x^2}}}{lnx-x}$,$x∈[{\frac{1}{e},e}]$,则$k'(x)=\frac{(x-1)(2lnx+x+2)}{{{{(lnx-x)}^2}}}$,
易得2lnx+x+2>0,
令k'(x)>0,解得x>1;令k'(x)<0,解得x<1,
故k(x)在$[\frac{1}{e},1)$递减,在(1,e]递增,
故k(x)的最大值是$k(\frac{1}{e})$或k(e),
而$k(\frac{1}{e})=-\frac{2e-1}{e(e+1)}<k(e)=\frac{e(e-2)}{e-1}$,
故$m≤\frac{e(e-2)}{e-1}$.
点评 本题考查函数的导数的应用,函数的最值以及函数的单调区间的求法,考查转化思想以及计算能力.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,4) | C. | (1,4] | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
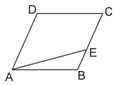 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )| A. | $\frac{1}{3}$ | B. | $\frac{9}{16}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com