
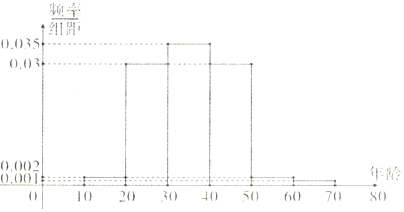
分析 (I)设x满足:(0.002+0.03+x)×10=$\frac{1}{2}$,解得x=0.018.可得中位数=30+$\frac{0.018}{0.035}$×10.
其平均数$\overline{a}$=15×0.02+25×0.3+35×0.35+45×0.3+55×0.02+65×0.01.
(II)由于现比赛进行到武亦姝和彭敏的得分比为3:2,可假设:武亦姝和彭敏的得分分别为3,2.则最终武亦姝获得冠军接下来有以下6种情况:
| 1 | 1 | ||
| 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
解答 解:(I)设x满足:(0.002+0.03+x)×10=$\frac{1}{2}$,解得x=0.018.
∴中位数=30+$\frac{0.018}{0.035}$×10≈35.14(岁).
其平均数$\overline{a}$=15×0.02+25×0.3+35×0.35+45×0.3+55×0.02+65×0.01=35.3.
(II)由于现比赛进行到武亦姝和彭敏的得分比为3:2,可假设:武亦姝和彭敏的得分分别为3,2.
则最终武亦姝获得冠军接下来有以下6种情况:
| 1 | 1 | ||
| 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{6}{10}$ | $\frac{3}{10}$ |
点评 本题考查了频率分布直方图的性质、中位数与平均数的计算公式、互斥事件与相互独立事件、超几何分布列的计算公式与数学期望、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
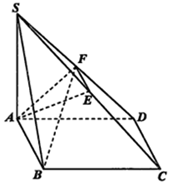 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com