
| A. | 3n-1 | B. | 2n-1+n2-1 | C. | 2n2-3n+2 | D. | n2 |
分析 对于任意n∈N*,A(n),B(n),C(n)成等差数列,可得:2B(n)=A(n)+C(n),化为:an+2-an+1=a2-a1=2,对于任意n∈N*都成立.可得数列{an}是等差数列.
解答 解:∵对于任意n∈N*,A(n),B(n),C(n)成等差数列,
∴2B(n)=A(n)+C(n),
∴2(a2+a3+…+an+1)=a1+a2+…+an+a3+a4+…+an+2,
化为:a2+an+1=a1+an+2,
即an+2-an+1=a2-a1=2,对于任意n∈N*都成立.
∴数列{an}是等差数列,首项为1,公差为2.
∴A(n)=a1+a2+…+an=$n+\frac{n(n-1)}{2}×2$=n2.
故选:D.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
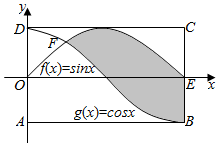 如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,则图中阴影部分的面积为( )
如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,则图中阴影部分的面积为( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -$\frac{1}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72n+1 | B. | 22n+1 | C. | 32n+1 | D. | 52n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com