练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知矩阵M=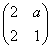,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P'(-4,0),

    (1)求实数a的值.

    (2)求矩阵M的特征值及其对应的特征向量.

     

    (1)3 (2) 矩阵M的属于特征值4的特征向量为(t≠0)

    【解析】(1)由=,得2-2a=-4⇒a=3.

    (2)由(1)知M=,则矩阵M的特征多项式为

    (λ-2)(λ-1)-6=λ2-3λ-4.

    令λ2-3λ-4=0,得矩阵M的特征值为-1或4.

    当λ=-1时,⇒x+y=0,

    ∴(x,y)=(t,- t),当t≠0时,

    矩阵M的属于特征值-1的特征向量为(t≠0);

    当λ=4时,⇒2x-3y=0,

    ∴矩阵M的属于特征值4的特征向量为(t≠0).

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷（解析版） 题型：选择题

    等差数列{an}的前n项和为Sn,已知am-1+am+1-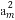=0,S2m-1=38,则m=(　　)

    (A)38(B)20(C)10(D)9

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷（解析版） 题型：解答题

    根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

    API

    0～50

    51～

    100

    101～

    150

    151～

    200

    201～

    250

    251～

    300

    >300

    级　别

    Ⅰ

    Ⅱ

    Ⅲ1

    Ⅲ2

    Ⅳ1

    Ⅳ2

    Ⅴ

    状　况

    优

    良

    轻微

    污染

    轻度

    污染

    中度

    污染

    中度

    重污染

    重度

    污染

     

    对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.

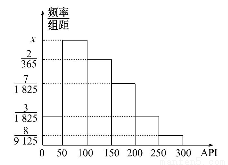
    (1)求直方图中x的值.

    (2)计算一年中空气质量分别为良和轻微污染的天数.

    (3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.

    (结果用分数表示.

    已知57=78125,27=128,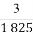++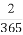++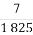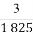=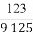,365=73×5).

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷（解析版） 题型：解答题

    已知在一个2×2矩阵M的变换作用下,点A(1,2)变成了点A'(4,5),点B(3,-1)变成了点B'(5,1).

    (1)求2×2矩阵M.

    (2)若在2×2矩阵M的变换作用下,点C(x,0)变成了点C'(4,y),求x,y.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷（解析版） 题型：解答题

    已知2×2矩阵M=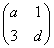有特征值λ=-1及对应的一个特征向量e1=.

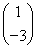    (1)求矩阵M.

    (2)设曲线C在矩阵M的作用下得到的方程为x2+2y2=1,求曲线C的方程.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷（解析版） 题型：解答题

    已知曲线C的极坐标方程为ρ2=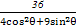,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.

    (1)求曲线C的直角坐标方程及参数方程.

    (2)若P(x,y)是曲线C上的一个动点,求x+2y的最小值,并求P点的坐标.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷（解析版） 题型：解答题

    设直线l1的参数方程为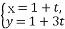(t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷（解析版） 题型：填空题

    设一次试验成功的概率为p,进行100次独立重复试验,当p=_______时,成功次数的标准差的值最大,其最大值为　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷（解析版） 题型：解答题

    一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.

    (1)若袋中共有10个球,

    ①求白球的个数;

    ②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.

    (2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于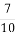,并指出袋中哪种颜色的球的个数最少.

     

    查看答案和解析>>

    同步练习册答案