考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由fn(x)=(x+n)•ex,得f′n(x)=(x+n+1)•ex.得当x=-(n+1)时,fn(x)取得极小值fn(-(n+1))=-e-(n+1).
(2)引进新函数h(x),确定单调区间,从而求出当n=3时,a-b取得最小值e-4,即a-b≥e-4.
(3)由条件可得φ(x)=x2+a|lnx-1|,分情况讨论①当x≥e时②当1≤x<e时,从而求出函数y=φ(x)的最小值,得出a的取值范围.
解答:
解:(1)f
n(x)=(x+n)•e
x(n∈N
*).
∵f
n(x)=(x+n)•e
x,
∴f′
n(x)=(x+n+1)•e
x.
∵x>-(n+1)时,f′
n(x)>0;x<-(n+1)时,f′
n(x)<0,
∴当x=-(n+1)时,f
n(x)取得极小值f
n(-(n+1))=-e
-(n+1).
(2)由题意 b=f
n(-(n+1))=-e
-(n+1),
又a=g
n(-n+1)=(n-3)
2,
∴a-b=(n-3)
2+e
-(n+1).
令h(x)=(x-3)
2+e
-(x+1)(x≥0),
则h′(x)=2(x-3)-e
-(x+1),
又h′(x)在区间[0,+∞)上单调递增,
∴h′(x)≥h′(0)=-6-e
-1.
又h′(3)=-e
-4<0,h′(4)=2-e
-5>0,
∴存在x
0∈(3,4)使得h′(x
0)=0.
∴当0≤x<x
0时,h′(x)<0;当x>x
0时,h′(x)>0.
即h(x)在区间[x
0,+∞)上单调递增,在区间[0,x
0)上单调递减,
∴h(x)
min=h(x
0).
又h(3)=e
-4,h(4)=1+e
-5,
∴h(4)>h(3),
∴当n=3时,a-b取得最小值e
-4,即a-b≥e
-4.
(3).由条件可得φ(x)=x
2+a|lnx-1|,
①当x≥e时,φ(x)=x
2+alnx-a,φ′(x)=2x+
,
∴φ(x)>0恒成立,
∴φ(x)在[e,+∞)上增函数,故当x=e时,y
min=φ(e)=e
2 ②当1≤x<e时,φ(x)=x
2-alnx+a,
∴φ′(x)=2x-
=
(x+
)(x-
),
(i)当
≤1即0<a≤2时,φ′(x)在x∈(1,e)为正数,
∴φ(x)在区间(1,e)上为增函数,
故当x=1时,y
min=1+a,且此时φ(1)<φ(e)=e
2;
(ii)当1<
<e,即2<a<2e
2时,φ′(x)在x∈(1,
)时为负数,在x∈(
,e)时为正数,
∴φ(x)在区间[1,
)上为减函数,在(
,e]上为增函数,
故当x=
时,y
min=
-
ln
,且此时φ(x)=e
2;
(iii)当
≥e,即:a≥2e
2时,φ′(x)在x∈(1,e)时为负数,
∴φ(x)在区间[1,e]上为减函数,
故当x=e时,ymin=φ(e)=e
2;
综上所述,函数y=φ(x)的最小值为:
ymin=
| | 1+a , 0<a≤2 | | -ln, 2<a≤2a2 | | e2 a>2e2 |
| |
,
所以当
1+a≥a时,得0<a≤2;
当
a-ln≥a(2<a<2e
2)时,无解;
当
e2≥a(a≥2e
2)时,得
a≤e不成立.
综上,所求a的取值范围是0<a≤2.
点评:本题考察了函数的单调性,求函数的最值问题,导数的应用,渗透了分类讨论思想,是一道综合性较强的问题.



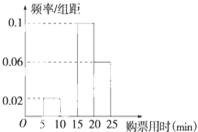 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).