
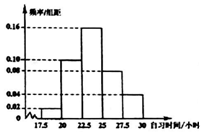
 某校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于24小时的人数是( )
某校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于24小时的人数是( )| A. | 76 | B. | 92 | C. | 108 | D. | 114 |
分析 由频率分布直方图求出自习时间在[17.5,24)内的频率为0.54,从而这200名学生中每周的自习时间不少于24小时的人数是:200×(1-0.54),由此能求出结果.
解答 解:由频率分布直方图得:
自习时间在[17.5,22.5)内的频率为(0.02+0.10)×2.5=0.3,
自习时间在[22.5,25)内的频率为0.16×2.5=0.4,
∴自习时间在[17.5,24)内的频率为:0.3+0.4×$\frac{24-22.5}{2.5}$=0.54,
∴这200名学生中每周的自习时间不少于24小时的人数是:200×(1-0.54)=92.
故选:B.
点评 本题考查频数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在正方体ABCD-A1B1C1D1中,O、O1分别为底面ABCD和A1B1C1D1的中心,以OO1所在直线为轴旋转线段BC1形成的几何体的正视图为( )
在正方体ABCD-A1B1C1D1中,O、O1分别为底面ABCD和A1B1C1D1的中心,以OO1所在直线为轴旋转线段BC1形成的几何体的正视图为( )| A. |  | B. |  | C. | 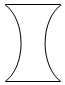 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在$\widehat{NM}$上,∠MON=$\frac{π}{3}$,ON=OM=$\sqrt{3}$.设∠DON=θ,矩形ABCD的面积为S.
某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在$\widehat{NM}$上,∠MON=$\frac{π}{3}$,ON=OM=$\sqrt{3}$.设∠DON=θ,矩形ABCD的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个社会调查机构就某地居民的月收入调查了100人,并根据所得数据画出了如图所示的频率分布直方图,则估计这100人的月平均收入为2400元.
一个社会调查机构就某地居民的月收入调查了100人,并根据所得数据画出了如图所示的频率分布直方图,则估计这100人的月平均收入为2400元.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{12}{5}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com