
| A. | (-∞,18) | B. | (-∞,18] | C. | [18,+∞) | D. | (18,+∞) |
分析 $\frac{{f({p+1})-f({q+1})}}{p-q}>2$恒成立$?\frac{{f({p+1})-f({q+1})}}{{({p+1})-({q+1})}}>2$恒成立?'f(x+1)≥2恒成立,即$\frac{a}{x+2}-2({x+1})≥2({0<x<1})$恒成立,分离参数,求最值,即可求出实数a的取值范围.
解答 解:因为f(x)=aln(x+1)-x2,所以f(x+1)=aln[(x+1)+1]-(x+1)2,
所以$f'({x+1})=\frac{a}{x+2}-2({x+1})$.
因为p,q∈(0,1),且p≠q,所以$\frac{{f({p+1})-f({q+1})}}{p-q}>2$恒成立$?\frac{{f({p+1})-f({q+1})}}{{({p+1})-({q+1})}}>2$恒成立
?'f(x+1)≥2恒成立,即$\frac{a}{x+2}-2({x+1})≥2({0<x<1})$恒成立,
所以a>2(x+2)2(0<x<1)恒成立,
又因为x∈(0,1)时,8<2(x+2)2<18,所以a≥18.
故选:C.
点评 本题考查导数知识的运用,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
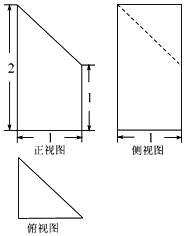
| A. | ${\frac{5}{6}_{\;}}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
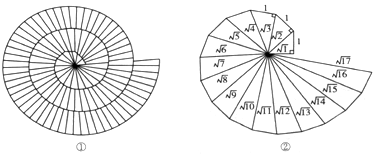
| A. | 120° | B. | 130° | C. | 135° | D. | 140° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
| 频数 | 5 | 9 | 11 | 9 | 7 | 9 |
| 满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
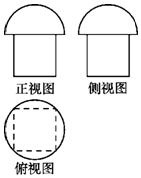 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com