
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
���� �������к�����ͼ�����ν�Ͻ����ж�����������
��� 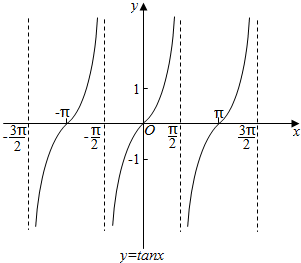 �⣺�������к�����ͼ������ͼ��
�⣺�������к�����ͼ������ͼ��
�������к�����ͼ��õ������к��������ں�������С�������ǦУ��ʢ���ȷ��
�������к�����ͼ�����ԭ��Գƣ��õ����к������溯�����ʢ���ȷ��
�����к�����ֵ����ʵ����R���ڶ������������ֵ����Сֵ���ʢ���ȷ��
�����к����ڣ�k$��-\frac{��}{2}$��$k��+\frac{��}{2}$����k��Z�����������������ڵ����ݼ����䣬�ʢ���ȷ��
��x=$\frac{��}{2}$+k�У�k��Z���������߲��ཻ���ʢ���ȷ��
���������������ĶԳ�ͼ�Σ���Գ����������ǣ�$\frac{k��}{2}$��0����k��Z���ʢ���ȷ��
��ѡ��D��
���� ���⿼��������ٵ��жϣ��ǻ����⣬����ʱҪ�������⣬ע�����к�����ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��b����ac��bc | B�� | ��a��b��c��d����ac��bd | ||
| C�� | ��a��b��0����$\frac{1}{a}$��$\frac{1}{b}$ | D�� | ��a��b����an��bn��n��N*��n��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��1 | B�� | b��-1��b��1 | C�� | -1��b��1 | D�� | b��1��b��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Բ�� | B�� | ��Բ�� | C�� | ��Բ�� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B�� | -$\frac{\sqrt{6}+\sqrt{2}}{4}$ | C�� | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D�� | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com