Question

17．某工厂制作如图所示的一种标识，在半径为R的圆内做一个关于圆心对称的“工”字图形，“工”字图形由横、竖、横三个等宽的矩形组成，两个横距形全等且成是竖矩形长的$\sqrt{3}$倍，设O为圆心，∠AOB=2α，“工”字图形的面积记为S．
（1）将S表示为α的函数；
（2）为了突出“工”字图形，设计时应使S尽可能大，则当α为何值时，S最大？

Answer 1

分析 （1）连接CD，取AB的中点M，连接OM，交CD于N，由解直角三角形可得AB=2Rsinα，BC=MN=OM-ON=R（cosα-$\frac{\sqrt{3}}{3}$sinα），α∈（0，$\frac{π}{3}$）），再由矩形的面积公式可得S=2AB•BC+$\frac{\sqrt{3}}{3}$AB•BC，即可得到所求；
（2）运用二倍角的正弦公式和余弦公式、以及两角和的正弦公式，运用正弦函数的值域，即可得到所求最大值．

解答 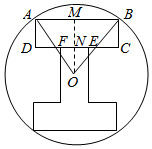解：（1）连接CD，取AB的中点M，连接OM，交CD于N，
由∠AOB=2α，可得∠BOM=α，α∈（0，$\frac{π}{2}$），
且BM=Rsinα，OM=Rcosα，由题意可得ON=$\frac{\sqrt{3}}{3}$BM=$\frac{\sqrt{3}}{3}$Rsinα，
BC=MN=OM-ON=R（cosα-$\frac{\sqrt{3}}{3}$sinα），
由BC＞0，可得α∈（0，$\frac{π}{3}$），
则S=2AB•BC+$\frac{\sqrt{3}}{3}$AB•BC=（4+$\frac{2\sqrt{3}}{3}$）R²（sinαcosα-$\frac{\sqrt{3}}{3}$sin²α），（α∈（0，$\frac{π}{3}$））；
（2）S=（4+$\frac{2\sqrt{3}}{3}$）R²（sinαcosα-$\frac{\sqrt{3}}{3}$sin²α）
=（4+$\frac{2\sqrt{3}}{3}$）R²（$\frac{1}{2}$sin2α+$\frac{\sqrt{3}}{6}$cos2α-$\frac{\sqrt{3}}{6}$）
=$\frac{\sqrt{3}}{3}$（4+$\frac{2\sqrt{3}}{3}$）R²（$\frac{\sqrt{3}}{2}$sin2α+$\frac{1}{2}$cos2α）-$\frac{\sqrt{3}}{6}$（4+$\frac{2\sqrt{3}}{3}$）R²
=$\frac{\sqrt{3}}{3}$（4+$\frac{2\sqrt{3}}{3}$）R²sin（2α+$\frac{π}{6}$）-$\frac{\sqrt{3}}{6}$（4+$\frac{2\sqrt{3}}{3}$）R²
由α∈（0，$\frac{π}{3}$），可得$\frac{π}{6}$＜2α+$\frac{π}{6}$＜$\frac{5π}{6}$，
即有2α+$\frac{π}{6}$=$\frac{π}{2}$，即α=$\frac{π}{6}$时，S取得最大值$\frac{1+2\sqrt{3}}{3}$R²．

点评 本题考查三角形函数的应用题的解法，考查三角函数的化简和求值，注意运用二倍角公式和两角和的正弦公式，考查正弦函数的值域的运用，属于中档题．