
【题目】已知函数![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)依据题设条件运用导数与函数单调性之间的关系分类求解;(2)先将不等式进行等价转化,再构造函数借助导数知识及分类整合思想分析求解:
(1)![]() ,
,
(ⅰ)当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ⅱ)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减.
单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,所以
,所以![]() ,即
,即![]() .
.
![]() 恒成立与
恒成立与![]() 恒成立等价,
恒成立等价,
令![]() ,即
,即![]() ,则
,则![]() ,
,
①当![]() 时,
时, ![]() (或令
(或令![]() ,则
,则![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() )
)
∴![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 恒成立,
恒成立,
②当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
又![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,故当
,故当![]() 时,
时, ![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上单调递增.
上单调递增.
∴![]() ,
,
即![]() ,
, ![]() 不恒成立,
不恒成立,
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.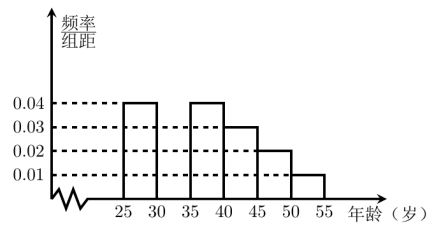
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 ,
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an , 求数列{ ![]() }的前n项和.
}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四凌锥S﹣ABCD中,底面ABCD是直角梯形,AD∥BC,SA⊥CD,AB⊥平面SAD,M是SC的中点,且SA=AB=BC=2,AD=1. 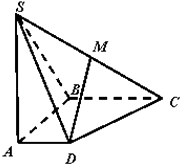
(1)求证:DM∥平面SAB;
(2)求四棱锥S﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:

①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子原件生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是一级品的概率;
(2)至少有一件二级品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象一个最高点为P(
)的图象一个最高点为P( ![]() ,2),相邻最低点为Q(
,2),相邻最低点为Q( ![]() ,﹣2),当x∈[﹣
,﹣2),当x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com